题目内容
20.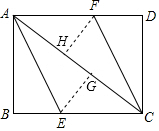 如图,在矩形ABCD中,AC是对角线,E、F分别在BC、AD边上,将边AB沿AE折叠,点B落在对角线AC上的G处,将边CD沿CF折叠,点D落在对角线AC上的点H处.
如图,在矩形ABCD中,AC是对角线,E、F分别在BC、AD边上,将边AB沿AE折叠,点B落在对角线AC上的G处,将边CD沿CF折叠,点D落在对角线AC上的点H处.(1)求证:四边形AECF是平行四边形.
(2)若AB=6,AC=10,求BE的长.
分析 (1)先证明△AEG≌△CFH,从而可证明AE=FC,且AE∥FC,最后依据平行四边形的判定定理进行证明即可;
(2)先利用勾股定理求得BC的长,设BE=x,则EC=8-x,然后再Rt△EGC中,依据勾股定理列方程求解即可.
解答 解:(1)由翻折的性质可知AB=AG,CH=DC,∠ABE=$\frac{1}{2}$∠BAG,∠FCH=$\frac{1}{2}$∠DCH.
又∵AB=CD,∠BAG=∠DCH,
∴AG=FC,∠EAG=∠FCH.
在△AEG和△FCH中,$\left\{\begin{array}{l}{∠EGA=∠FHC}\\{AG=CH}\\{∠EAG=∠FCH}\end{array}\right.$,
∴△AEG≌△FCH.
∴AE=CF,∠EAG=∠FCH.
∴AE∥FC.
∴四边形AECF是平行四边形.
(2)∵AB=6 AC=10,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=8.
设BE=x,则EG=x,EC=8-x.
∵AG=AB=6,
∴CG=4.
∵EG2+GC2=EC2,
∴x2+42=(8-x)2,解得x=3
∴BE=3.
点评 本题主要考查的是翻折的性质、矩形的性质、平行四边形的判定、勾股定理的应用,依据勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知命题A:“带根号的数都是无理数”.在下列选项中,可以作为判断“命题A是假命题”的反例的是( )
| A. | $\sqrt{3}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{8}$ |
11.下列说法正确的是( )
| A. | 对角线相等的四边形是平行四边形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线互相垂直的四边形是平行四边形 | |
| D. | 对角线互相垂直且相等的四边形是平行四边形 |
8.下列命题正确的是( )
| A. | △ABC中,∠A、∠B、∠C的对边分别为a、b、c.若a2+b2=c2 则∠B=90° | |
| B. | 如果一个三角形两边的平方差等于第三边的平方,那么这个三角形是直角三角形 | |
| C. | 直角三角形中,两条边的平方和等于第三边的平方 | |
| D. | △ABC中,若a=3、b=4则c=5 |
 在如图所示的长方体中,AB=2,BC=2,高CG=4.则从点A到点G的最短路线长为4$\sqrt{2}$.
在如图所示的长方体中,AB=2,BC=2,高CG=4.则从点A到点G的最短路线长为4$\sqrt{2}$.
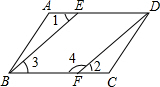 如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据: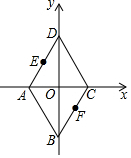 以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,若AD的中点E的坐标为(a,b),则BC的中点F的坐标为(-a,-b).
以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,若AD的中点E的坐标为(a,b),则BC的中点F的坐标为(-a,-b).