题目内容
2.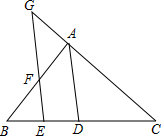 如图,在△ABC中,AD平分∠BAC,交BC于点D,点G在CA的延长线上,GE交AB,BC于点F,E,且∠BFE=∠G.
如图,在△ABC中,AD平分∠BAC,交BC于点D,点G在CA的延长线上,GE交AB,BC于点F,E,且∠BFE=∠G.求证:AD∥GE.
分析 首先根据角平分线的性质可得∠BAC=2∠DAC,再根据三角形外角与内角的关系可得∠G+∠GFA=∠BAC,又∠AFG=∠G.进而得到∠BAC=2∠G,从而得到∠DAC=∠G,即可判定出AD∥GE.
解答 证明:∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠BFE=∠G,∠BFE=∠GFA,
∵∠G+∠GFA=∠BAC,∠AFG=∠G.
∴∠BAC=2∠G,
∴∠DAC=∠G,
∴AD∥GE.
点评 此题主要考查了平行线的判定,关键是掌握三角形内角与外角的关系,以及平行线的判定定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知命题A:“带根号的数都是无理数”.在下列选项中,可以作为判断“命题A是假命题”的反例的是( )
| A. | $\sqrt{3}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{8}$ |
7.已知矩形ABCD中,AB=2$\sqrt{3}$-$\sqrt{2}$,BC=$\sqrt{6}$+1,则矩形ABCD的面积是( )
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{3}$-$\sqrt{2}$ | C. | 5$\sqrt{2}$-4$\sqrt{3}$ | D. | 5$\sqrt{2}$+4$\sqrt{3}$ |
11.下列说法正确的是( )
| A. | 对角线相等的四边形是平行四边形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线互相垂直的四边形是平行四边形 | |
| D. | 对角线互相垂直且相等的四边形是平行四边形 |
 如图,在矩形ABCD中,连接对角线AC,BD,延长BC至点E,使BC=CE,连接DE.求证:DE=AC.
如图,在矩形ABCD中,连接对角线AC,BD,延长BC至点E,使BC=CE,连接DE.求证:DE=AC. 如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF.
如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF.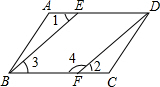 如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据: