题目内容
5. 如图,菱形ABCD的周长为20,对角线AC与BD相交于点O,AC=8,则BD=6.
如图,菱形ABCD的周长为20,对角线AC与BD相交于点O,AC=8,则BD=6.
分析 根据菱形的四条边都相等可得AB=5,根据菱形的两条对角线互相垂直且平分可得AC⊥BD,AO=$\frac{1}{2}$AC=4,BO=DO,再利用勾股定理计算出BO长,进而可得答案.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=$\frac{1}{2}$AC=4,BO=DO,AD=AB=DC=BC,
∵菱形ABCD的周长为20,
∴AB=5,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=3,
∴DO=3,
∴DB=6,
故答案为:6.
点评 此题主要考查了菱形的性质,关键是掌握菱形的性质 ①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.

练习册系列答案
相关题目
13.方程2x=-6的解是( )
| A. | x=3 | B. | x=4 | C. | x=-3 | D. | x=-4 |
10.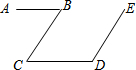 如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
 如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )| A. | 40° | B. | 60° | C. | 140° | D. | 160° |
9. 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 某公司销售智能机器人,每台售价为10万元,进价y(万元)与销量x(台)之间的函数关系的图象如图所示.
某公司销售智能机器人,每台售价为10万元,进价y(万元)与销量x(台)之间的函数关系的图象如图所示.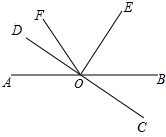 如图,直线AB与CD相交于点O,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF,则∠EOC=90°.
如图,直线AB与CD相交于点O,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF,则∠EOC=90°.