题目内容
18.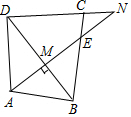 如图,在四边形ABCD中,AD=CD,∠ADC=90°,N为DC的延长线上一点,AN⊥BD于点M,交BC于点E,且∠BAN=45°,下列结论:
如图,在四边形ABCD中,AD=CD,∠ADC=90°,N为DC的延长线上一点,AN⊥BD于点M,交BC于点E,且∠BAN=45°,下列结论:①∠CBD=45°;②$\sqrt{2}$BD-AB=BC;③若BE=2CE,则S△BCD=6S△CEN.
其中结论正确的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①正确.由△DOC∽△AOB,推出$\frac{DO}{AO}$=$\frac{CO}{OB}$,推出$\frac{DO}{CO}$=$\frac{AO}{OB}$,由∠DOA=∠COB,推出△AOD∽△BOC,推出∠CBO=∠DAO=45°即可.
②正确.如图2中,将△DCB绕点D顺时针旋转得到△DAK.只要证明K、A、B共线,△KDB是等腰直角三角形,即可解决问题.
③正确.如图3中,作DH⊥BC于H,DK⊥BA于K,NG⊥BC于G.设EC=a,BE=2a,则AB=BE=2a,BD=$\frac{AB+BC}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$a,AM=BM=$\sqrt{2}$a,DM=$\frac{3\sqrt{2}}{2}$a,想办法求出DH、NG即可解决问题.
解答 解:①正确.理由:如图1中,连接AC.
∵DA=DC,∠ADC=90°,
∴∠DCO=∠DAC=45°,
∵AN⊥BD,∠BAN=45°,
∴∠OBA=∠DCO=45°,∵∠DOC=∠AOB,
∴△DOC∽△AOB,
∴$\frac{DO}{AO}$=$\frac{CO}{OB}$,
∴$\frac{DO}{CO}$=$\frac{AO}{OB}$,
∵∠DOA=∠COB,
∴△AOD∽△BOC,
∴∠CBO=∠DAO=45°,即∠CBD=45°.
②正确.理由:如图2中,将△DCB绕点D顺时针旋转得到△DAK.
∵∠ADC+∠ABC=180°,
∴∠DAB+∠DCB=180°,
∵∠DAK=∠DCB,
∴∠DAK+∠DAB=180°,
∴K、A、B共线,
∵∠K=∠DBC=∠DBK=45°,
∴△KDB是等腰直角三角形,
∴BK=$\sqrt{2}$BD,
∵BK=AK+AB=BC+AB,
∴$\sqrt{2}$BD=AB+BC,即$\sqrt{2}$BD-AB=BC.
③正确.理由:如图3中,作DH⊥BC于H,DK⊥BA于K,NG⊥BC于G.设EC=a,BE=2a,则AB=BE=2a,BD=$\frac{AB+BC}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$a,AM=BM=$\sqrt{2}$a,DM=$\frac{3\sqrt{2}}{2}$a,
∵∠DBH=∠DBK,DK⊥BA,DH⊥BC,
∴DK=DH,∵DA=DC,
∴△DKA≌△DHC(HL),
∴AK=CH,BK=BH=$\frac{5}{2}$a,AK=CH=$\frac{1}{2}$a,
∴AD=DC=$\sqrt{(\frac{5}{2}a)^{2}+(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{26}}{2}$a,
由△DMN∽△AMD,得$\frac{DN}{AD}$=$\frac{DM}{AM}$,
∴DN=$\frac{3}{4}$$\sqrt{26}$a,CN=$\frac{\sqrt{26}}{4}$,
∵NG∥DH,
∴$\frac{NG}{DH}$=$\frac{CN}{DC}$,
∴NG=$\frac{5}{4}$a,
∴$\frac{{S}_{△BDC}}{{S}_{△CEN}}$=$\frac{\frac{1}{2}•3a•\frac{5}{2}a}{\frac{1}{2}•a•\frac{5}{4}a}$=$\frac{1}{6}$,
∴S△BCD=6S△CEN.
故选D.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形或全等三角形解决问题,属于中考选择题中的压轴题.

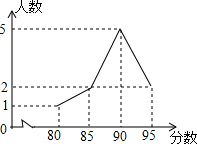 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
| 进球数n(个) | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进n个球的人数 | 1 | 2 | 7 | 9 | 3 | 2 |
| A. | 4或-3 | B. | 4 | C. | -3 | D. | 3 |
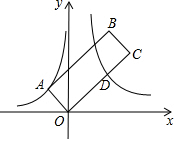 如图,双曲线y=-$\frac{2}{x}$与y=$\frac{6}{x}$分别过矩形ABCO上的A、D两点,OD=2CD,矩形ABCO面积为18$\sqrt{3}$,则OC的长为( )
如图,双曲线y=-$\frac{2}{x}$与y=$\frac{6}{x}$分别过矩形ABCO上的A、D两点,OD=2CD,矩形ABCO面积为18$\sqrt{3}$,则OC的长为( )| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $9\sqrt{3}$ |
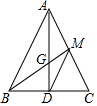 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.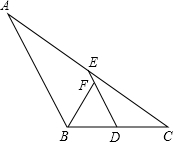 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是3.
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是3. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为6.
如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为6.