题目内容
11.如图,用同样规格的规格黑白两色正方形瓷砖铺设矩形地面,请观察图形并解答有关问题.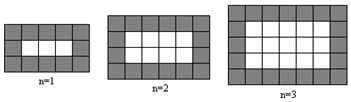
(1)在第n个图中,每一横行共有n+4块瓷砖,每竖行共有n+2块瓷砖(均用含n的代数式表示)
(2)设铺设地面所用的瓷砖总块数y,写出y与n的函数关系式(不写n的取值范围)
(3)按上述铺设方案,铺一块这样的地面共用了528块瓷砖,求此时n的值.
分析 (1)第一个图每一横行有5=1+4个瓷砖,竖列有3=1+2个瓷砖;第二个图每一横行有6=2+4个瓷砖,竖列有4=2+2个瓷砖;第n个图每一横行有n+4个瓷砖,竖列有n+2个瓷砖.
(2)根据(1)中横行和数列的瓷砖数,总数=横行的瓷砖数×竖列的瓷砖数.
(3)根据(2)列的关系式将528代入其中求解.
解答 解:(1)通过观察得:n=1时,横行有1+4块,竖列有1+2块,
n=2时,横行有2+4块,竖列有2+2块,
n=3时,横行有3+4块,竖列有3+2块,
…,
所以在第n个图中,每一横行共有n+4块,每一竖列共有n+2块,
故答案为:n+4,n+2;
(2)由(1)可得总块数可表示为y=(n+4)(n+2);
(3)根据题意可得(n+4)(n+2)=528,
解得:n=20或n=-26,
∴n=20.
点评 此题考查一元二次方程的应用及图形的变化规律,找出图形之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
5.九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
6.某班进行个人投篮比赛,受污损的表记录了在规定时间内投进几个球的人数分布情况.已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均每人投进2.5个球,则投进3个球的有9人,投进4个球的有3人.
| 进球数n(个) | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进n个球的人数 | 1 | 2 | 7 | 9 | 3 | 2 |
1.下列各数中,最小的数是( )
| A. | 0 | B. | 3 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
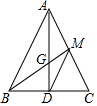 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.