题目内容
20. 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):| 运动员 环数 次数 | 1 | 2 | 3 | 4 | 5 |
| 甲 | 10 | 8 | 9 | 10 | 8 |
| 乙 | 10 | 9 | 9 | a | b |
S甲2=$\frac{1}{5}$[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=17;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.
分析 (1)根据表中数据描点、连线即可得;
(2)根据平均数的定义列出算式,整理即可得;
(3)由a+b=17得b=17-a,将其代入到S甲2<S乙2,即$\frac{1}{5}$[(10-9)2+(9-9)2+(9-9)2+(a-9)2+(b-9)2]>0.8,得到a2-17a+71>0,求出a的范围,根据a、b均为整数即可得出答案.
解答 解:(1)如图所示: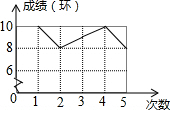
(2)由题意知,$\frac{10+9+9+a+b}{5}$=9,
∴a+b=17,
故答案为:17;
(3)∵甲比乙的成绩较稳定,
∴S甲2<S乙2,即$\frac{1}{5}$[(10-9)2+(9-9)2+(9-9)2+(a-9)2+(b-9)2]>0.8,
∵a+b=17,
∴b=17-a,
代入上式整理可得:a2-17a+71>0,
解得:a<$\frac{17-\sqrt{5}}{2}$或a>$\frac{17+\sqrt{5}}{2}$,
∵a、b均为整数,
∴a=7、b=10;a=10、b=7.
点评 本题主要考查折线统计图、平均数、方差,熟练掌握平均数和方差的计算公式及解一元二次不等式是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
11.甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
| 统计量 | 甲 | 乙 | 丙 | 丁 |
| 平均数 | 9.2 | 9.2 | 9.2 | 9.2 |
| 方差 | 0.60 | 0.62 | 0.50 | 0.44 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
8.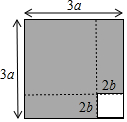 如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
 如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )| A. | 3a+2b | B. | 3a+4b | C. | 6a+2b | D. | 6a+4b |
5.正整数x、y满足(2x-5)(2y-5)=25,则x+y等于( )
| A. | 18或10 | B. | 18 | C. | 10 | D. | 26 |
5.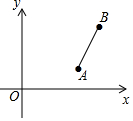 已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
 已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )| A. | (1,2) | B. | (2,1) | C. | (7,0) | D. | (1,3) |
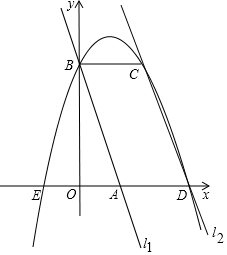 如图,在平面直角坐标系中2条直线为l1:y=-3x+3,l2:y=-3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
如图,在平面直角坐标系中2条直线为l1:y=-3x+3,l2:y=-3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中: 已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.
已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.