题目内容
5.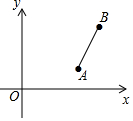 已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )| A. | (1,2) | B. | (2,1) | C. | (7,0) | D. | (1,3) |
分析 过点B作BD垂直于过点A与x轴的平行线于D,过点C作CE垂直于过点A与x轴的平行线于E,根据点A、B的坐标求出AD、BD,然后求出△ABD和△CAE全等,根据全等三角形对应边相等可得CE=AD,AE=BD,然后求解即可.
解答  解:如图,过点B作BD垂直于过点A与x轴的平行线于D,过点C作CE垂直于过点A与x轴的平行线于E,
解:如图,过点B作BD垂直于过点A与x轴的平行线于D,过点C作CE垂直于过点A与x轴的平行线于E,
∵A(4,1),B(5,4),
∴AD=5-4=1、
BD=4-1=3,
∵线段AB绕点A逆时针旋转90°得线段AC,
∴AB=AC,∠CAB=90°,
∴∠CAE+∠BAD=90°,
又∵∠B+∠BAD=90°,
∴∠B=∠CAE,
在△ABD和△CAE中,$\left\{\begin{array}{l}{∠B=∠CAE}\\{∠D=∠E=90°}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴CE=AD=1,AE=BD=3,
∴点C的横坐标为:4-3=1,
纵坐标为:1+1=2,
∴点C的坐标为(1,2).
故选A.
点评 本题考查了坐标与图形变化-旋转,全等三角形的判定与性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.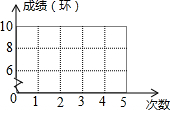 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
某同学计算出了甲的成绩平均数是9,方差是
S甲2=$\frac{1}{5}$[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=17;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.
 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):| 运动员 环数 次数 | 1 | 2 | 3 | 4 | 5 |
| 甲 | 10 | 8 | 9 | 10 | 8 |
| 乙 | 10 | 9 | 9 | a | b |
S甲2=$\frac{1}{5}$[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=17;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.
13.一组数据5,1,x,6,4的众数是4,这组数据的方差是( )
| A. | $\sqrt{2}$ | B. | 2.8 | C. | 2 | D. | $\sqrt{10}$ |
20.2016年深圳市生产总值同比增长9%,记作+9%,而尼日利亚国内生产总值同比下滑2.24%,应记作( )
| A. | 2.24% | B. | -2.24% | C. | 2.24 | D. | -2.24 |
10.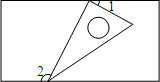 如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
 如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )| A. | 100° | B. | 105° | C. | 110° | D. | 120° |
17.下列运算正确的是( )
| A. | (-a)4=a4 | B. | 8a-a=8 | C. | a3×a2=a6 | D. | (a-b)2=a2-b2 |
15.若x<y,则下列不等式中不成立的是( )
| A. | x-1<y-1 | B. | 3x<3y | C. | $\frac{x}{2}$<$\frac{y}{2}$ | D. | -2x<-2y |
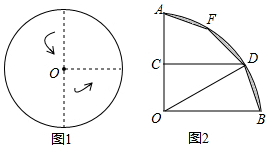 如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.
如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.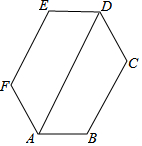 如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )