题目内容
8．
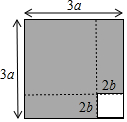如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（ ）| A． | 3a+2b | B． | 3a+4b | C． | 6a+2b | D． | 6a+4b |
分析 观察图形可知，这块矩形较长的边长=边长为3a的正方形的边长-边长2b的小正方形的边长+边长2b的小正方形的边长的2倍，依此计算即可求解．
解答 解：依题意有
3a-2b+2b×2
=3a-2b+4b
=3a+2b．
故这块矩形较长的边长为3a+2b．
故选：A．
点评 考查了列代数式，关键是得到这块矩形较长的边长与两个正方形边长的关系．
练习册系列答案
阅读快车系列答案
相关题目
18．计算$\frac{{{{（{x+y}）}^2}-{{（{x-y}）}^2}}}{4xy}$的结果为（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | 0 |
19．下列计算正确的是（ ）
| A． | $\sqrt{（-4）^{2}}$=2 | B． | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | C． | （$\sqrt{2}$）2=4 | D． | $\sqrt{6}$÷$\sqrt{2}$=3 |
16．已知点A（1，y1），B（2，y2），C（-3，y3）都在反比例函数y=$\frac{{{k^2}+1}}{x}$的图象上，则y1，y2，y3的大小关系是（ ）
| A． | y3＜y1＜y2 | B． | y1＜y2＜y3 | C． | y2＜y1＜y3 | D． | y3＜y2＜y1 |
13．
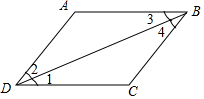如图，若∠A+∠ABC=180°，则下列结论正确的是（ ）
如图，若∠A+∠ABC=180°，则下列结论正确的是（ ）| A． | ∠1=∠2 | B． | ∠2=∠3 | C． | ∠1=∠3 | D． | ∠2=∠4 |
20．
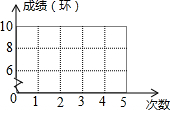甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：
某同学计算出了甲的成绩平均数是9，方差是
S甲2=$\frac{1}{5}$[（10-9）2+（8-9）2+（9-9）2+（10-9）2+（8-9）2]=0.8，请作答：
（1）在图中用折线统计图将甲运动员的成绩表示出来；
（2）若甲、乙射击成绩平均数都一样，则a+b=17；
（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由．
甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：| 运动员 环数 次数 | 1 | 2 | 3 | 4 | 5 |
| 甲 | 10 | 8 | 9 | 10 | 8 |
| 乙 | 10 | 9 | 9 | a | b |
S甲2=$\frac{1}{5}$[（10-9）2+（8-9）2+（9-9）2+（10-9）2+（8-9）2]=0.8，请作答：
（1）在图中用折线统计图将甲运动员的成绩表示出来；
（2）若甲、乙射击成绩平均数都一样，则a+b=17；
（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由．
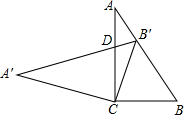在Rt△ABC中，∠C=90°，cosB=0.6，把这个直角三角形绕顶点C旋转后得到Rt△A'B'C，其中点B'正好落在AB上，A'B'与AC相交于点D，那么B′D：CD=0.35．
13．一组数据5，1，x，6，4的众数是4，这组数据的方差是（ ）
| A． | $\sqrt{2}$ | B． | 2.8 | C． | 2 | D． | $\sqrt{10}$ |