题目内容
10．
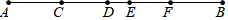如图，C、D、E、F为线段AB上顺次排列的4个动点（不与A、B重合），图中共有15条线段．若AB=8.6cm，DE=1cm，图中所有线段长度之和为56cm，则线段CF长为4cm．
分析 可以设出线段CF的长，再根据图中所有线段的长度之和为56cm，即可列出方程，解方程即可求出答案．
解答 解：5+4+3+2+1=15（条）
设线段CF的长为xcm，依题意有
8.6×5+3x+1=56，
解得x=4．
答：图中共有15条线段，线段CF长为4cm．
故答案为：15，4．
点评 本题考查了两点间的距离，有一定难度，根据题意列出方程式，并探讨解的合理性是关键．
练习册系列答案
相关题目
20．某工厂生产一种合金薄板（其厚度忽略不计），这些薄板的形状均为正方形，边长（单位：cm）在5～50（含5和50）之间，每张薄板的成本价（单位：元）与它的面积（单位：cm2）成正比例，每张薄板的出厂价（单位：元）由基础价和浮动价两部分组成，其中基础价与薄板的大小无关，是固定不变的，浮动价与薄板的边长成正比例，在营销过程中得到了表格中的数据：
（1）求一张薄板的出厂价y与边长x之间满足的函数关系式，并写出自变量的取值范围；
（2）已知出厂一张边长为40cm的薄板，获得利润是26元（利润=出厂价-成本价）．
①求一张薄板的利润W与边长x这之间满足的函数关系式；
②当边长为多少厘米时，出厂一张薄板获得的利润最大？最大利润是多少元？
| 薄板的边长（cm） | 20 | 30 |
| 出厂价（元/张） | 50 | 70 |
（2）已知出厂一张边长为40cm的薄板，获得利润是26元（利润=出厂价-成本价）．
①求一张薄板的利润W与边长x这之间满足的函数关系式；
②当边长为多少厘米时，出厂一张薄板获得的利润最大？最大利润是多少元？
如图，BD是△ABC的角平分线，点E、F分别在BC、AB上，且DE∥AB，EF∥AC．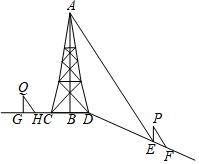
如图，在斜坡顶部有一铁塔AB，B是CD的中点，CD是水平的．在阳光的照射下，塔影DE留在斜坡面上．在同一时刻，小明站在点E处，其影子EF在直线DE上，小华站在点G处，影子GH在直线CD上，他们的影子长分别为2m和1m．已知CD=12m，DE=18m，小明和小华身高均为1.6m，那么塔高AB为多少？
19．若关于x的一元二次方程kx2-4x+1=0有实数根，则k的取值范围是（ ）
| A． | k=4 | B． | k＞4 | C． | k≤4且k≠0 | D． | k≤4 |
