题目内容
15.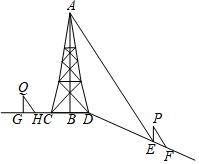 如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?
如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?
分析 过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AN,GB长,把它们相加即可.
解答 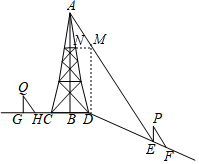 解:过D作DF⊥CD,交AE于点M,过M作MN⊥AB,垂足为N.
解:过D作DF⊥CD,交AE于点M,过M作MN⊥AB,垂足为N.
由题意得:$\frac{DM}{DE}$=$\frac{1.6}{2}$.
∴DM=DE×1.6÷2=14.4(m).
∴MN=BD=$\frac{1}{2}$CD=6m.
又∵$\frac{AN}{MN}$=$\frac{1.6}{1}$.
∴AN=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
点评 本题考查了运用所学的解直角三角形的知识解决实际生活中的问题,要求我们要具备数学建模能力(即将实际问题转化为数学问题).

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
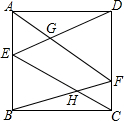 如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.
如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.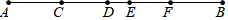 如图,C、D、E、F为线段AB上顺次排列的4个动点(不与A、B重合),图中共有15条线段.若AB=8.6cm,DE=1cm,图中所有线段长度之和为56cm,则线段CF长为4cm.
如图,C、D、E、F为线段AB上顺次排列的4个动点(不与A、B重合),图中共有15条线段.若AB=8.6cm,DE=1cm,图中所有线段长度之和为56cm,则线段CF长为4cm.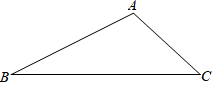 如图,已知△ABC,请用尺规作图,在BC上找一点M,使得AM+MC=BC(保留作图痕迹,不写作法).
如图,已知△ABC,请用尺规作图,在BC上找一点M,使得AM+MC=BC(保留作图痕迹,不写作法).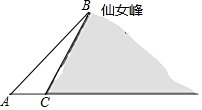 数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)
数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)