题目内容
先阅读再解答:
(1)如图1,AB∥CD,试说明:∠B+∠D=∠BED.
可以考虑把∠BED变成两个角的和.过E点引一条直线EF∥AB,则有∠B=∠1,再设法证明∠D=∠2,需证EF∥CD,这可通过已知AB∥CD和EF∥AB得到.
(2)已知:如图2,AB∥CD,求证:∠BED=360°-(∠B+∠D).
(3)已知:如图3,AB∥CD,∠ABF=∠DCE.求证:∠BFE=∠FEC.
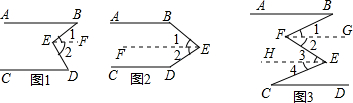
(1)如图1,AB∥CD,试说明:∠B+∠D=∠BED.
可以考虑把∠BED变成两个角的和.过E点引一条直线EF∥AB,则有∠B=∠1,再设法证明∠D=∠2,需证EF∥CD,这可通过已知AB∥CD和EF∥AB得到.
(2)已知:如图2,AB∥CD,求证:∠BED=360°-(∠B+∠D).
(3)已知:如图3,AB∥CD,∠ABF=∠DCE.求证:∠BFE=∠FEC.

考点:平行线的性质
专题:
分析:(2)过点E作EF∥AB,根据同旁内角互补,可得出结论;
(3)作EG∥CD,根据(1)的结论,以及平行线的性质可以证得.
(3)作EG∥CD,根据(1)的结论,以及平行线的性质可以证得.
解答:证明:(2)如图2,过点E作EF∥AB,则EF∥AB∥CD,
∴∠ABE+∠1=180°,∠2+∠EDC=180°,
∴∠ABE+∠1+∠2+∠EDC=360°.
即:∠BED=360°-(∠B+∠D).
(3)如图3,作FG∥AB.EG∥CD,则∠B=∠1,∠C=∠4.
∵AB∥CD,
∴FG∥GE,
∴∠2=∠3,
∴∠1+∠2=∠3+∠4,
即:∠BFE=∠FEC.
∴∠ABE+∠1=180°,∠2+∠EDC=180°,
∴∠ABE+∠1+∠2+∠EDC=360°.
即:∠BED=360°-(∠B+∠D).
(3)如图3,作FG∥AB.EG∥CD,则∠B=∠1,∠C=∠4.
∵AB∥CD,
∴FG∥GE,
∴∠2=∠3,
∴∠1+∠2=∠3+∠4,
即:∠BFE=∠FEC.
点评:本题考查了平行线的性质;正确作出辅助线和角的等量代换的运用是正确解答本题的关键.

练习册系列答案
相关题目
 如图,在直角坐标系中,△ABC的顶点坐标是A(-1,2),B(-3,1),C(0,-1).将△ABC向右平移2个单位,向下平移3个单位得到△A1B1C1,将△A1B1C1绕O点旋转90°得到△A2B2C2.
如图,在直角坐标系中,△ABC的顶点坐标是A(-1,2),B(-3,1),C(0,-1).将△ABC向右平移2个单位,向下平移3个单位得到△A1B1C1,将△A1B1C1绕O点旋转90°得到△A2B2C2.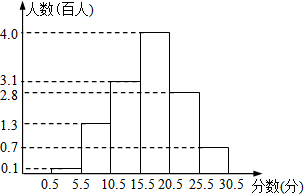 2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答:
2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答: