题目内容
（1）已知10a=5，10b=6，求102a-3b的值．
（2）已知x=7，求1-x-x（1-x）-x（1-x）2-…-x（1-x）2009的值．
（2）已知x=7，求1-x-x（1-x）-x（1-x）2-…-x（1-x）2009的值．
考点：整式的混合运算—化简求值
专题：
分析：（1）先根据同底数幂进行变形，在根据幂的乘方变形，最后代入求出即可；
（2）先提公因式，再提公因式，得出规律，最后代入求出即可．
（2）先提公因式，再提公因式，得出规律，最后代入求出即可．
解答：解：（1）∵10a=5，10b=6，
∴102a-3b
=102a÷103b
=（10a）2÷（10b）3
=52÷63
=
；
（2）∵x=7，
∴1-x-x（1-x）-x（1-x）2-…-x（1-x）2009
=（1-x）[1-x-x（1-x）-x（1-x）2-…-x（1-x）2008]
=（1-x）（1-x）[1-x-x（1-x）2-…-x（1-x）2007]
=（1-x）2009
=（1-7）2009
=62009．
∴102a-3b
=102a÷103b
=（10a）2÷（10b）3
=52÷63
=
| 25 |
| 216 |
（2）∵x=7，
∴1-x-x（1-x）-x（1-x）2-…-x（1-x）2009
=（1-x）[1-x-x（1-x）-x（1-x）2-…-x（1-x）2008]
=（1-x）（1-x）[1-x-x（1-x）2-…-x（1-x）2007]
=（1-x）2009
=（1-7）2009
=62009．
点评：本题考查了整式的混合运算和求值，同底数幂的除法，幂的乘方，提公因式的应用，主要考查学生的计算能力，题目比较好，难度适中．
练习册系列答案
相关题目
已知某三角形三边分别是m2-n2、2mn、m2+n2（m＞n），且m、n都是整数，此三角形是（ ）
| A、直角三角形 |
| B、等腰直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
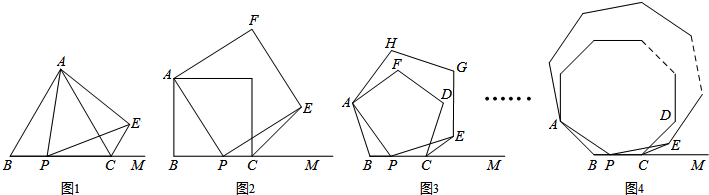
数学课上，同学们探究下面命题的正确性：顶角为36°的