题目内容
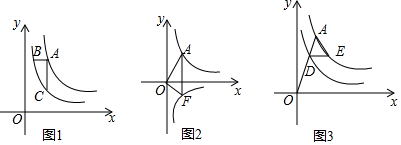
7.点A是双曲线y=$\frac{4}{x}$(x>0)上一点.(1)如图1,若AB∥x轴,AC∥y轴,AB,AC分别交双曲线y=$\frac{1}{x}$于B,C两点,若AC=3,求AB的长;
(2)如图2,若AF∥y轴,交双曲线y=$-\frac{1}{x}$(x>0)于F点,连接AO,FO,且OF⊥OA,求AF的长;
(3)如图3,连接OA交双曲线y=$\frac{1}{x}$(x>0)于D点,DE∥x轴交y=$\frac{4}{x}$(x>0)的图象于E,求△ADE的面积.
分析 设出点A的坐标,
(1)先表示出C的坐标,进而得出AC=$\frac{3}{m}$,由AC=3建立方程求出m的值,即可得出AB;
(2)先表示出F的坐标,进而得出AF,利用勾股定理建立方程即可求出m的值即可得出结论;
(3)先确定出OA解析式,设出点D的坐标,进而用m表示出点D的坐标,E的坐标,最后用三角形的面积公式即可得出结论.
解答 解:设A(m,$\frac{4}{m}$)(m>0),
(1)∵AC∥y轴,点C在y=$\frac{1}{x}$的图象上,
∴C(m,$\frac{1}{m}$),
∴AC=$\frac{4}{m}$-$\frac{1}{m}$=$\frac{3}{m}$=3,
∴m=1,
∵AB∥x轴,点B在y=$\frac{1}{x}$的图象上,
∴($\frac{m}{4}$,$\frac{4}{m}$),
∴AB=m-$\frac{m}{4}$=$\frac{3}{4}$m=$\frac{3}{4}$;
(2)∴AF∥y轴,点F在y=-$\frac{1}{x}$的图象上,
∴F(m,-$\frac{1}{m}$),
∴AF=$\frac{4}{m}$-(-$\frac{1}{m}$)=$\frac{5}{m}$,
∵OF⊥OA,
∴△AOF是直角三角形,
∴OA2+OF2=AF2,
∴m2+$\frac{16}{{m}^{2}}$+m2+$\frac{1}{{m}^{2}}$=$\frac{25}{{m}^{2}}$,
∴m=-$\sqrt{2}$(舍)或m=$\sqrt{2}$,
∴AF=$\frac{5}{m}$=$\frac{5\sqrt{2}}{2}$;
(3)∵A(m,$\frac{4}{m}$),
∴直线OA的解析式为y=$\frac{4}{{m}^{2}}$x,
设D(n,$\frac{1}{n}$)(n>0),
∵点D在直线OA上,
∴$\frac{1}{n}=\frac{4}{{m}^{2}}×n$,
∴m2=4n2,
∵m>0,n>0,
∴m=2n,
∴D($\frac{m}{2}$,$\frac{2}{m}$),
∵DE∥x轴,点E在y=$\frac{4}{x}$的图象上,
∴E(2m,$\frac{2}{m}$),
∴DE=$\frac{3}{2}$m,
∴S△ADE=$\frac{1}{2}$DE×($\frac{4}{m}$-$\frac{2}{m}$)=$\frac{1}{2}$×$\frac{3}{2}$m×$\frac{2}{m}$=$\frac{3}{2}$.
点评 此题是反比例函数综合题,主要考查了反比例函数的性质,直角三角形的性质,待定系数法,三角形的面积公式,解本题的关键是用反比例函数的解析式表示出点的坐标,是一道简单题目.

 阅读快车系列答案
阅读快车系列答案| A. | y=$\frac{2}{x}$ | B. | y=$\frac{-2}{x}$ | C. | y=-2x+4 | D. | y=4+2x |
| A. | 已知圆心 | B. | 已知半径 | ||
| C. | 过三个已知点 | D. | 过一个三角形的三个顶点 |
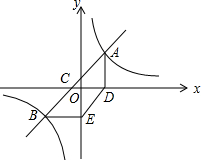 如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.
如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,y=S1+S2,则y与x的关系式是y=-x2+3x.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,y=S1+S2,则y与x的关系式是y=-x2+3x.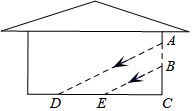 如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.
如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.