题目内容
1. 如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.
如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.
分析 由在?ABCD中,BE平分∠ABC,CE平分∠BCD,易证得△ABE与△DCE是等腰三角形,△BCE是直角三角形,然后可得AD=2AB,由勾股定理可求得BC的长,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,AB=CD,
∴∠ABC+∠BCD=180°,∠AEB=∠EBC,∠DEC=∠ECB,
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABE=∠EBC=$\frac{1}{2}$∠ABC,∠DCE=∠ECB=$\frac{1}{2}$∠BCD,
∴∠EBC+∠ECB=90°,∠ABE=∠AEB,∠DEC=∠DCE,
∴∠BEC=90°,AB=AE,DE=CD,
∴AB=CD=AE=DE=$\frac{1}{2}$AD,
∵BE=4,CE=3,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=5,
∴AD=5,
∴AB=2.5.
故答案为:2.5.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及勾股定理.注意证得△ABE与△DCE是等腰三角形,△BCE是直角三角形是关键.

练习册系列答案
相关题目
6.已知一次函数y=-x+1与反比例函数y=-$\frac{2}{x}$,x,y一些对应值如表:
那么不等式-x+1<-$\frac{2}{x}$(x<0)的解为-1<x<0.
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=-x+1 | … | 4 | 3 | 2 | 0 | -1 | -2 | … |
| y=-$\frac{2}{x}$ | … | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ | … |
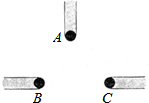 (1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?
(1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?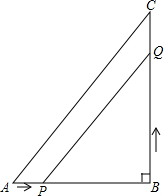 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB方向以1cm/s的速度移动,点Q从点B开始,沿BC方向以2cm/s的速度移动.若点P,Q分别从A点,B点同时出发,几秒钟后,PQ=$\sqrt{5}$AP?
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB方向以1cm/s的速度移动,点Q从点B开始,沿BC方向以2cm/s的速度移动.若点P,Q分别从A点,B点同时出发,几秒钟后,PQ=$\sqrt{5}$AP?