题目内容
6．已知一次函数y=-x+1与反比例函数y=-$\frac{2}{x}$，x，y一些对应值如表：| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=-x+1 | … | 4 | 3 | 2 | 0 | -1 | -2 | … |
| y=-$\frac{2}{x}$ | … | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ | … |
分析 先判断出交点坐标，进而判断在交点的哪侧相同横坐标时一次函数的值都小于反比例函数的值即可．
解答 解：从对应值表可以考查一次函数和反比例函数的两个交点为（-1，2），（2，-1），经过观察可得在交点（-1，2）的右边，y轴的左侧，相同横坐标时一次函数的值都小于反比例函数的值，所以 不等式-x+1＜-$\frac{2}{x}$（x＜0）的解为-1＜x＜0．
故答案为-1＜x＜0．
点评 本题考查了一次函数和反比例函数的交点问题，给出相应的函数值，求自变量的取值范围应该从交点入手思考．
练习册系列答案
同步练习强化拓展系列答案
相关题目
画出函数y1=-2x-3和函数y2=3x+2的图象，根据图象指出x取什么值时，y1＜y2？
如图，在?ABCD中，BE平分∠ABC，CE平分∠BCD，若BE=4，CE=3，则AB的长为2.5．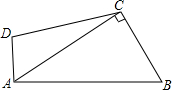
如图，在四边形ABCD中，AB=4$\sqrt{3}$，∠DAB=90°，∠B=60°，AC⊥BC，
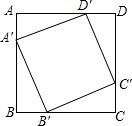已知，如图，点A′、B′、C′、D′分别在正方形的边AB、BC、CD、DA上且AA′=BB′=CC′=DD′．