题目内容
13.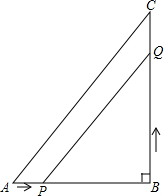 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB方向以1cm/s的速度移动,点Q从点B开始,沿BC方向以2cm/s的速度移动.若点P,Q分别从A点,B点同时出发,几秒钟后,PQ=$\sqrt{5}$AP?
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB方向以1cm/s的速度移动,点Q从点B开始,沿BC方向以2cm/s的速度移动.若点P,Q分别从A点,B点同时出发,几秒钟后,PQ=$\sqrt{5}$AP?
分析 设x秒钟后,PQ=$\sqrt{5}$AP.由AP=xcm,AB=6cm,BQ=2xcm,可得PB=(6-x)cm.在直角△BPQ中,利用勾股定理求出PQ2=PB2+BQ2=5x2-12x+36,再根据PQ=$\sqrt{5}$AP,列出方程5x2-12x+36=5x2,解方程即可.
解答 解:设x秒钟后,PQ=$\sqrt{5}$AP.
∵AP=xcm,AB=6cm,BQ=2xcm,
∴PB=(6-x)cm.
在直角△BPQ中,由勾股定理得
PQ2=PB2+BQ2=(6-x)2+(2x)2=5x2-12x+36,
∵PQ=$\sqrt{5}$AP,
∴5x2-12x+36=5x2,
解得x=3.
即若点P,Q分别从A点,B点同时出发,3秒钟后,PQ=$\sqrt{5}$AP.
点评 本题考查了几何动点问题在方程中的应用,勾股定理的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
3.一汽车租赁公司拥有某种型号的汽车100辆,公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如表关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式
(2)已知租出的车每辆每月需要维护费150元,未租出的车辆每月需要维护费50元,当租金定为3500元时,试求公司月收益为多少?
(3)根据市场调查报告,公司需要使每月出租的车辆不低于80辆,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
| x | 3000 | 3050 | 3100 | 3150 | 3200 | 3250 | 3300 |
| y | 100 | 99 | 98 | 97 | 96 | 95 | 94 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车辆每月需要维护费50元,当租金定为3500元时,试求公司月收益为多少?
(3)根据市场调查报告,公司需要使每月出租的车辆不低于80辆,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
 如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.
如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.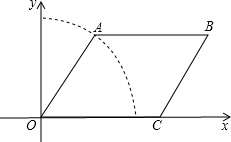 如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.
如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.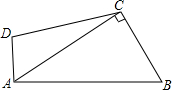 如图,在四边形ABCD中,AB=4$\sqrt{3}$,∠DAB=90°,∠B=60°,AC⊥BC,
如图,在四边形ABCD中,AB=4$\sqrt{3}$,∠DAB=90°,∠B=60°,AC⊥BC,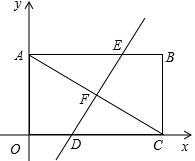 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.