题目内容
16.先化简再求值:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷($\frac{12}{x+2}$-x+2)+$\frac{1}{x+4}$,其中,x为该不等式组$\left\{\begin{array}{l}{x-2<0}\\{5x+1>2(x-1)}\end{array}\right.$的整数解.分析 先解不等式组,求得x的值,根据运算顺序,先算括号里面的,分子、分母分别有理化,再约分即可,把x的值代入计算即可.
解答 解:解不等式得,-1<x<2,
则x=0或1,
原式=$\frac{(x-4)^{2}}{x(x+2)}$×$\frac{x+2}{(4+x)(4-x)}$+$\frac{1}{x+4}$
=$\frac{4-x}{x(x+4)}$+$\frac{1}{x+4}$
=$\frac{4}{x(x+4)}$
当x=0时,原式无意义,
当x=1时,原式=$\frac{4}{5}$.
点评 本题考查了分式的化简求值,解这类题的关键是利用分解因式的方法化简分式,特别注意运算顺序及符号的处理.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.某快餐公司最新推出A、B两种营养配餐,成本价分别为5元/份和10元/份,近两周的销售情况如下表:
(1)求A、B两种营养配餐的销售价格分别为多少元?
(2)若快餐公司准备6000元资金全部用来购买制作A、B两种快餐的原材料,考虑市场需要,要求制作的B种快餐的数量不少于A种快餐数量的2倍.那么该快餐公司至少要制作B种快餐多少份?
(3)在(2)的条件下,该快餐公司要获得最大利润,那么要制作B种快餐多少份?最大利润是多少元?
| 销售时段 | A种配餐销售量 | B种配餐销售量 | 销售额 |
| 第一周 | 100份 | 300份 | 5500元 |
| 第二周 | 200份 | 400份 | 8000元 |
(2)若快餐公司准备6000元资金全部用来购买制作A、B两种快餐的原材料,考虑市场需要,要求制作的B种快餐的数量不少于A种快餐数量的2倍.那么该快餐公司至少要制作B种快餐多少份?
(3)在(2)的条件下,该快餐公司要获得最大利润,那么要制作B种快餐多少份?最大利润是多少元?
 如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.
如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.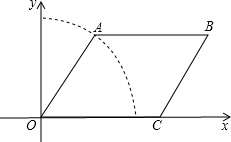 如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.
如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.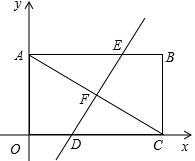 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.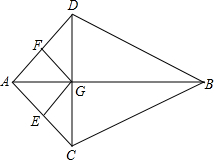 如图,AB是CD的垂直平分线,交CD于点G,过点G分别作GE⊥AC于E,GF⊥AD于F
如图,AB是CD的垂直平分线,交CD于点G,过点G分别作GE⊥AC于E,GF⊥AD于F