题目内容
12.菱形ABCD中,∠B=60°,AB=4,点P在BC上,连接AP,将线段AP绕点P顺时针旋转60°,交CD于点E,当PC=1时,CE=3.分析 过点E作EF⊥BC于点F,过点P作PG⊥AB于点G,先根据菱形的性质求出BG、PG和AG的长,进而求出tan∠2的值,然后根据1+∠APE=∠2+∠B,∠APE=∠B=60°,即可得到∠CEF=30°,再设CF=x,则CE=2x,EF=$\sqrt{3}$x,利用三角形函数值求出x的值,即可求出CE的长.
解答  解:过点E作EF⊥BC于点F,过点P作PG⊥AB于点G,
解:过点E作EF⊥BC于点F,过点P作PG⊥AB于点G,
∵∠B=60°,
∴BG=BPcos60°=3×$\frac{1}{2}$=$\frac{3}{2}$,
∴PG=$\frac{3\sqrt{3}}{2}$,AG=AB-BG=4-$\frac{3}{2}$=$\frac{5}{2}$,
∴tan∠2=$\frac{PG}{AG}$=$\frac{\frac{3\sqrt{3}}{2}}{\frac{5}{2}}$=$\frac{3\sqrt{3}}{5}$,
又∵∠1+∠APE=∠2+∠B,∠APE=∠B=60°,
∴∠1=∠2,
∵∠DCF=60°,
∴∠CEF=30°,
设CF=x,则CE=2x,EF=$\sqrt{3}$x,
∴tan∠1=$\frac{EF}{PF}$=$\frac{\sqrt{3}x}{1+x}$=$\frac{3\sqrt{3}}{5}$,
∴x=$\frac{3}{2}$,
∴CE=2x=3,
故答案为3.
点评 本题主要考查了菱形的性质的知识,解答本题的关键是正确地作出辅助线,求出tan∠2的值,此题有一定的难度.

练习册系列答案
相关题目
3.一汽车租赁公司拥有某种型号的汽车100辆,公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如表关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式
(2)已知租出的车每辆每月需要维护费150元,未租出的车辆每月需要维护费50元,当租金定为3500元时,试求公司月收益为多少?
(3)根据市场调查报告,公司需要使每月出租的车辆不低于80辆,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
| x | 3000 | 3050 | 3100 | 3150 | 3200 | 3250 | 3300 |
| y | 100 | 99 | 98 | 97 | 96 | 95 | 94 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车辆每月需要维护费50元,当租金定为3500元时,试求公司月收益为多少?
(3)根据市场调查报告,公司需要使每月出租的车辆不低于80辆,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
7.某快餐公司最新推出A、B两种营养配餐,成本价分别为5元/份和10元/份,近两周的销售情况如下表:
(1)求A、B两种营养配餐的销售价格分别为多少元?
(2)若快餐公司准备6000元资金全部用来购买制作A、B两种快餐的原材料,考虑市场需要,要求制作的B种快餐的数量不少于A种快餐数量的2倍.那么该快餐公司至少要制作B种快餐多少份?
(3)在(2)的条件下,该快餐公司要获得最大利润,那么要制作B种快餐多少份?最大利润是多少元?
| 销售时段 | A种配餐销售量 | B种配餐销售量 | 销售额 |
| 第一周 | 100份 | 300份 | 5500元 |
| 第二周 | 200份 | 400份 | 8000元 |
(2)若快餐公司准备6000元资金全部用来购买制作A、B两种快餐的原材料,考虑市场需要,要求制作的B种快餐的数量不少于A种快餐数量的2倍.那么该快餐公司至少要制作B种快餐多少份?
(3)在(2)的条件下,该快餐公司要获得最大利润,那么要制作B种快餐多少份?最大利润是多少元?
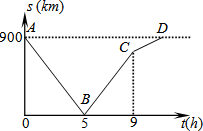 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.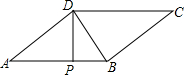 如图,?ABCD中,DP⊥AB于P,且PD2=AP•PB,△BCD的面积和周长分别为24和24,求PD的长.
如图,?ABCD中,DP⊥AB于P,且PD2=AP•PB,△BCD的面积和周长分别为24和24,求PD的长. 如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.
如图,在?ABCD中,BE平分∠ABC,CE平分∠BCD,若BE=4,CE=3,则AB的长为2.5.