题目内容
5．
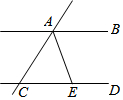如图，直线AB∥CD，AE平分∠CAB．AE与CD相交于点E，∠ACD=50°，则∠BAE的度数是（ ）| A． | 50° | B． | 65° | C． | 70° | D． | 130° |
分析 先由平行线性质得出∠ACD与∠BAC互补，并根据已知∠ACD=50°计算出∠BAC的度数，再根据角平分线性质求出∠BAE的度数．
解答 解：∵AB∥CD，
∴∠ACD+∠BAC=180°，
∵∠ACD=50°，
∴∠BAC=180°-50°=130°，
∵AE平分∠CAB，
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×130°=65°，
故选B．
点评 本题考查了平行线的性质和角平分线的定义，做好本题要熟练掌握：两直线平行，同旁内角互补．
练习册系列答案
名校课堂系列答案
相关题目
15．下列运算中不正确的是（ ）
| A． | a3+a2=a5 | B． | a3•a2=a5 | C． | a3÷a2=a | D． | （a3）2=a6 |
16．已知二次函数y=ax2+bx+c（a＞0）的图象过点A（1，n），B（3，n），若点C（-1．y1），D（0，y2），E（6，y3）也在该二次函数图象上，则下列结论正确的是（ ）
| A． | y1＜y2＜y3 | B． | y2＜y1＜y3 | C． | y3＜y1＜y2 | D． | y1＜y3＜y2 |
13．
如图，CE是△ABC的外角∠ACD的平分线，若∠B=25°，∠ACE=60°，则∠A=（ ）
如图，CE是△ABC的外角∠ACD的平分线，若∠B=25°，∠ACE=60°，则∠A=（ ）| A． | 105° | B． | 95° | C． | 85° | D． | 25° |
20．某校7个班同学积极捐出自己的零花钱献爱心，各班捐款的数额分别是（单位：元）：500，200，500，300，500，250，1350．这组数据的众数和中位数分别是（ ）
| A． | 500，200 | B． | 500，500 | C． | 500，300 | D． | 1350，500 |
10．下列运算正确的是（ ）
| A． | sin60°=$\frac{\sqrt{2}}{2}$ | B． | a6÷a2=a3 | C． | （-2）0=2 | D． | （2a2b）3=8a6b3 |
17．在某中学举行的“筑梦路上”演讲比赛中，八年级5名参赛选手的成绩分别为：90，93，89，90，88．关于这5名选手的成绩，下列说法正确的是（ ）
| A． | 平均数是89 | B． | 众数是93 | C． | 中位数是89 | D． | 方差是$\frac{14}{5}$ |
14．
如图，矩形ABCD的两条对角线相交于点O，∠AOB=120°，AD=2，点E是BC的中点，连结OE，则OE的长是（ ）
如图，矩形ABCD的两条对角线相交于点O，∠AOB=120°，AD=2，点E是BC的中点，连结OE，则OE的长是（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2 | D． | 4 |
15．计算$\frac{1}{3}$-$\frac{1}{2}$的结果是（ ）
| A． | 6的倒数 | B． | 6的相反数 | C． | -6的绝对值 | D． | -6的倒数 |