题目内容
14. 如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
分析 求出AB的长,由三角形中位线定理求出OE的长即可.
解答 解:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,BC=AD=3,∠ABC=90°,
∵∠AOB=120°,
∴∠BOC=60°,
∴△BOC是等边三角形,
∴∠BCO=60°,
∴AB=$\sqrt{3}$BC=2$\sqrt{3}$,
∵点E是BC的中点,
∴OE=$\frac{1}{2}$AB=$\sqrt{3}$;
故选:A.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理、三角形的中位线定理;熟练掌握矩形的性质和三角形中位线定理是关键.

练习册系列答案
相关题目
4.2的倒数是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
5.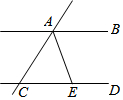 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )
 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )| A. | 50° | B. | 65° | C. | 70° | D. | 130° |
2. 如图,直线a直线b被直线c所截,且a∥b,若∠1=40°,则∠2的度数是( )
如图,直线a直线b被直线c所截,且a∥b,若∠1=40°,则∠2的度数是( )
 如图,直线a直线b被直线c所截,且a∥b,若∠1=40°,则∠2的度数是( )
如图,直线a直线b被直线c所截,且a∥b,若∠1=40°,则∠2的度数是( )| A. | 30° | B. | 60° | C. | 120° | D. | 140° |
9.下列各式能用平方差公式计算的是( )
| A. | (-a+b)(-a-b) | B. | (a+b)(a-2b) | C. | (-a+b)(a-b) | D. | (-a-b)(a+b) |
19.若a=2,则a2-2a+4的值为( )
| A. | -4 | B. | 4 | C. | 8 | D. | 12 |
6.生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程如图所示(阴影部分表示纸条反面),如果折成图丁形状的纸条宽 x cm,并且一端超出P点1cm,另一端超出P点2cm,那么折成的图丁所示的平面图形的面积为( )cm2.


| A. | $\frac{7}{2}{x^2}+3x$ | B. | $\frac{9}{2}{x^2}+3x$ | C. | $\frac{5}{2}{x^2}+3x$ | D. | 4x2+3x |
3.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示为( )
| A. | 0.3×105 | B. | 3×105 | C. | 0.3×106 | D. | 3×106 |
 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{2}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{2}$,则k的值为( )