题目内容
16.已知二次函数y=ax2+bx+c(a>0)的图象过点A(1,n),B(3,n),若点C(-1.y1),D(0,y2),E(6,y3)也在该二次函数图象上,则下列结论正确的是( )| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
分析 先利用抛物线的对称性得到抛物线的对称轴为直线x=2,然后根据二次函数的性质,通过比较点C、D、E到对称轴的距离的大小判断y1、y2、y3的大小.
解答 解:∵抛物线点A(1,n),B(3,n),
∴抛物线的对称轴为直线x=2,
∵点C(-1.y1)到直线x=2的距离为3,点D(0,y2)到直线x=2的距离为2,点E(6,y3)到直线x=1的距离为4,
而抛物线的开口向上,
∴y2<y1<y3.
故选B.
点评 本题考查了二次函数图象上点的坐标特征:熟练掌握二次函数的性质,利用二次函数的性质比较函数值的大小.

练习册系列答案
相关题目
6.如果函数y=ax2+2x+1的图象不经过第四象限,那么实数a的取值范围为( )
| A. | a<0 | B. | a=0 | C. | a>0 | D. | a≥0 |
7.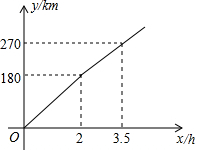 某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
 某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )| A. | 汽车在高速公路上的行驶速度为100km/h | |
| B. | 普通公路总长为90km | |
| C. | 汽车在普通公路上的行驶速度为60km/h | |
| D. | 汽车出发后4h到B地 |
4.2的倒数是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
11.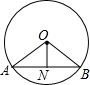 如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
 如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )| A. | 11 | B. | 9 | C. | 7 | D. | 5 |
1.样本数据3,2,5,a,4的众数与中位数相同,则a的值是( )
| A. | 2或3 | B. | 4或5 | C. | 3或4 | D. | 2或5 |
8.$\sqrt{3}$的倒数是( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
5.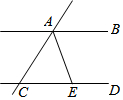 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )
 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=50°,则∠BAE的度数是( )| A. | 50° | B. | 65° | C. | 70° | D. | 130° |
6.生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程如图所示(阴影部分表示纸条反面),如果折成图丁形状的纸条宽 x cm,并且一端超出P点1cm,另一端超出P点2cm,那么折成的图丁所示的平面图形的面积为( )cm2.


| A. | $\frac{7}{2}{x^2}+3x$ | B. | $\frac{9}{2}{x^2}+3x$ | C. | $\frac{5}{2}{x^2}+3x$ | D. | 4x2+3x |