题目内容

13．如图，CE是△ABC的外角∠ACD的平分线，若∠B=25°，∠ACE=60°，则∠A=（　　）
A．105°B．95°C．85°D．25°

分析 先根据角平分线的性质求出∠ACD的度数，再由三角形外角的性质即可得出结论．

解答 解：∵CE是△ABC的外角∠ACD的平分线，∠ACE=60°，
∴∠ACD=2∠ACE=120°．
∵∠B=25°，
∴∠A=120°-25°=95°．
故选B．

点评 本题考查的是三角形外角的性质，熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键．

练习册系列答案
相关题目
3．tan30°的值为（　　）
A．1B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{3}$D．$\frac{\sqrt{3}}{2}$
4．2的倒数是（　　）
A．-2B．-$\frac{1}{2}$C．2D．$\frac{1}{2}$
1．样本数据3，2，5，a，4的众数与中位数相同，则a的值是（　　）
A．2或3B．4或5C．3或4D．2或5
8．$\sqrt{3}$的倒数是（　　）
A．-$\sqrt{3}$B．$\sqrt{3}$C．-$\frac{\sqrt{3}}{3}$D．$\frac{\sqrt{3}}{3}$
18．下列运算正确的是（　　）
A．a2+a3=a5B．a2•a3=a6C．（a2）3=a8D．a3÷a2=a
5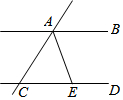．如图，直线AB∥CD，AE平分∠CAB．AE与CD相交于点E，∠ACD=50°，则∠BAE的度数是（　　）
A．50°B．65°C．70°D．130°
2．如图，直线a直线b被直线c所截，且a∥b，若∠1=40°，则∠2的度数是（　　）
A．30°B．60°C．120°D．140°
3．据报道，某小区居民李先生改进用水设备，在十年内帮助他居住小区的居民累计节水300 000吨．将300 000用科学记数法表示为（　　）
A．0.3×105B．3×105C．0.3×106D．3×106

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网