题目内容
12.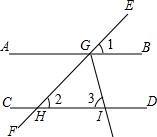 如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )| A. | 40° | B. | 50° | C. | 55° | D. | 70° |
分析 根据邻补角的性质与∠1=50°,求得∠BGH=180°-40°=140°,由GI平分∠HGB交直线CD于点I,得出∠BGI的度数,根据同位角相等,两直线平行,得到AB∥CD,从而利用平行线的性质,求得∠3的度数.
解答  解:∵∠1=50°,
解:∵∠1=50°,
∴∠BGH=180°-40°=140°,
∵GI平分∠HGB,
∴∠BGI=70°,
∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
∴∠3=∠BGI=70°(两直线平行,内错角相等).
故选D.
点评 本题主要考查了平行线的性质:两直线平行,内错角相等;以及平行线的判定方法:同位角相等,两直线平行.

练习册系列答案
相关题目
2.已知直线l同旁的两点A、B,在l上求一点P,使PA+PB最小,则求P点的作法正确的为( )
| A. | 作A关于l的对称点A′,连接A′B交l与P | |
| B. | AB的延长线与l交于P | |
| C. | 作A关于l的对称点A′,连接AA′交l与P | |
| D. | 以上都不对 |
20.当x=2时,(x2-x)-2(x2-x-1)的值等于( )
| A. | 4 | B. | -4 | C. | 1 | D. | 0 |
17.下列图象可能是函数y=mx+n与y=mnx的是( )
| A. |  | B. |  | C. |  | D. |  |
4.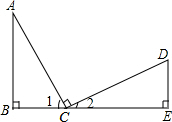 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | AB=CD |
1.一元二次方程y2=-6y的解是( )
| A. | -6 | B. | 0 | C. | 6 | D. | 0或-6 |
2.化简|$\sqrt{2}$-2|+$\sqrt{2}$-1的结果为( )
| A. | 2$\sqrt{2}$+1 | B. | 1 | C. | 2$\sqrt{2}$-1 | D. | -1 |
 如图所示,在△ABC中,∠A:∠B:∠BCA=1:2:3,CD⊥AB于D,AB=12,则DB等于( )
如图所示,在△ABC中,∠A:∠B:∠BCA=1:2:3,CD⊥AB于D,AB=12,则DB等于( ) 如图,在△ABC中,∠ABC=90°,D是AC上一点,AD=AB.若∠A=50°,则∠DBC=25°.
如图,在△ABC中,∠ABC=90°,D是AC上一点,AD=AB.若∠A=50°,则∠DBC=25°.