题目内容
2．已知直线l同旁的两点A、B，在l上求一点P，使PA+PB最小，则求P点的作法正确的为（ ）| A． | 作A关于l的对称点A′，连接A′B交l与P | |
| B． | AB的延长线与l交于P | |
| C． | 作A关于l的对称点A′，连接AA′交l与P | |
| D． | 以上都不对 |
分析 先作对称点A′，根据对称轴是对称点连线的垂直平分线可知：直线l是AA′的垂直平分线，根据垂直平分线的性质得：PA=PA′，所以PA+PB=PA′+PB，根据两点之间，线段最短得出点P就是所求作的点．
解答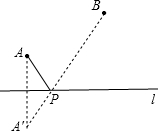 
解：作法：①作A关于l的对称点A′，则PA+PB=PA′+PB，
②连接A′B交l与P，
则P就是所求作的点；
根据两点之间，线段最短，可知：此时PA+PB最小；
故选A．
点评 本题是轴对称的最短路线问题，解题思路为：①根据轴对称的性质，作其中一个点的对称点，②与另一点相连接，与直线（对称轴）的交点就是所求作的点；把不在同一直线上的两条线段转化到一条直线上，结合两点之间线段最短，得出结论．
练习册系列答案
相关题目
13．方程2x2-4x+1=0化成（x+m）2=n（n≥0）的形式是（ ）
| A． | （x-1）2=$\frac{1}{2}$ | B． | （2x-1）2=$\frac{1}{2}$ | C． | （x-1）2=0 | D． | （x-2）2=3 |
在正△ABC内有一点P，PA=2，PB=2$\sqrt{3}$，PC=4，则CB的长为2$\sqrt{7}$．
17．下列所表示的数轴正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．如果向东走10米记作+10米，那么-5米表示（ ）
| A． | 向南走5米 | B． | 向西走-5米 | C． | 向西走5米 | D． | 向东走5米 |
14．
如图所示，AB是⊙O的弦，AB的长为24cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则OP的长的范围是（ ）
如图所示，AB是⊙O的弦，AB的长为24cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则OP的长的范围是（ ）| A． | 5≤OP≤12 | B． | 5≤OP≤10 | C． | 5≤OP≤13 | D． | 5≤OP≤24 |
12．
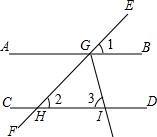如图，直线EF分别与直线AB、CD相交于点G、G，已知∠1=∠2=40°，GI平分∠HGB交直线CD于点I，则∠3=（ ）
如图，直线EF分别与直线AB、CD相交于点G、G，已知∠1=∠2=40°，GI平分∠HGB交直线CD于点I，则∠3=（ ）| A． | 40° | B． | 50° | C． | 55° | D． | 70° |