题目内容
4.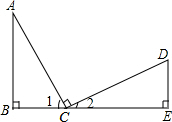 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | AB=CD |
分析 利用同角的余角相等求出∠A=∠2,再利用“角角边”证明△ABC和△CDE全等,根据全等三角形对应边相等,对应角相等,即可解答.
解答 解:∵∠B=∠E=90°,
∴∠A+∠1=90°,∠D+∠2=90°,
∵AC⊥CD,
∴∠1+∠2=90°,
∴∠A=∠2,故B正确;
∴∠A+∠D=90°,故A正确;
在△ABC和△CED中,
$\left\{\begin{array}{l}{∠A=∠2}\\{∠B=∠E}\\{AC=CD}\end{array}\right.$,
∴△ABC≌△CED(AAS),故C正确;
∴AB=CE,故D错误.
故选:D
点评 本题考查了全等三角形的判定与性质,等角的余角相等的性质,熟练掌握三角形全等的判定方法并确定出全等的条件∠A=∠2是解题的关键.

练习册系列答案
相关题目
14. 如图所示,AB是⊙O的弦,AB的长为24cm,点P是弦AB上一动点,且到圆心的最短距离为5cm,则OP的长的范围是( )
如图所示,AB是⊙O的弦,AB的长为24cm,点P是弦AB上一动点,且到圆心的最短距离为5cm,则OP的长的范围是( )
 如图所示,AB是⊙O的弦,AB的长为24cm,点P是弦AB上一动点,且到圆心的最短距离为5cm,则OP的长的范围是( )
如图所示,AB是⊙O的弦,AB的长为24cm,点P是弦AB上一动点,且到圆心的最短距离为5cm,则OP的长的范围是( )| A. | 5≤OP≤12 | B. | 5≤OP≤10 | C. | 5≤OP≤13 | D. | 5≤OP≤24 |
12.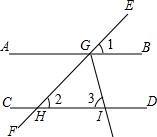 如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
 如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )| A. | 40° | B. | 50° | C. | 55° | D. | 70° |
19.下列条件不能判定△ABC为直角三角形的是( )
| A. | ∠A:∠B:∠C=1:2:3 | B. | a:b:c=1:1:$\sqrt{2}$ | C. | a:b:c=3:4:5 | D. | a:b:c=2:2:3 |
9.下列方程中,有实数解的是( )
| A. | $\sqrt{x-1}$+4=0 | B. | $\sqrt{{x}^{2}+1}$=0 | C. | $\sqrt{2x+3}$=-x | D. | $\sqrt{2x-3}$+$\sqrt{x+3}$=0 |
16.如果$\sqrt{a(a-4)}$=$\sqrt{a}$•$\sqrt{a-4}$,则( )
| A. | a≥4 | B. | a≥0 | C. | 0≤a≤4 | D. | a为一切实数 |
13.三角形的一边长为3xcm,这条边上的高为xcm,其面积为ycm2,则y与x的函数关系是( )
| A. | y=x2 | B. | y=2x2 | C. | y=$\frac{1}{2}$x2 | D. | y=$\frac{3}{2}$x2 |