题目内容
1．一元二次方程y2=-6y的解是（ ）| A． | -6 | B． | 0 | C． | 6 | D． | 0或-6 |
分析 利用因式分解法解方程即可解决问题．
解答 解：∵y2+6y=0，
∴y（y+6）=0，
∴y=0或-6．
故选D．
点评 本题考查一元二次方程的解，解题的关键是理解方程的解的定义，学会利用因式分解法解方程，属于基础题，中考常考题型．
练习册系列答案
阅读快车系列答案
相关题目
12．
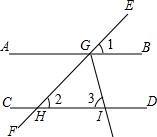如图，直线EF分别与直线AB、CD相交于点G、G，已知∠1=∠2=40°，GI平分∠HGB交直线CD于点I，则∠3=（ ）
如图，直线EF分别与直线AB、CD相交于点G、G，已知∠1=∠2=40°，GI平分∠HGB交直线CD于点I，则∠3=（ ）| A． | 40° | B． | 50° | C． | 55° | D． | 70° |
9．下列方程中，有实数解的是（ ）
| A． | $\sqrt{x-1}$+4=0 | B． | $\sqrt{{x}^{2}+1}$=0 | C． | $\sqrt{2x+3}$=-x | D． | $\sqrt{2x-3}$+$\sqrt{x+3}$=0 |
16．如果$\sqrt{a（a-4）}$=$\sqrt{a}$•$\sqrt{a-4}$，则（ ）
| A． | a≥4 | B． | a≥0 | C． | 0≤a≤4 | D． | a为一切实数 |
6．计算：（-2）101+（-2）100的结果是（ ）
| A． | -2 | B． | -2100 | C． | 2 | D． | 2100 |
13．三角形的一边长为3xcm，这条边上的高为xcm，其面积为ycm2，则y与x的函数关系是（ ）
| A． | y=x2 | B． | y=2x2 | C． | y=$\frac{1}{2}$x2 | D． | y=$\frac{3}{2}$x2 |
如图，等边△ABC的边长为4，AD是BC边上的中线，M是AD上的动点，E是AC边上的中点，则（EM+CM）2的最小值为（ ）
11．
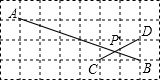如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD交于点P，则tan∠APC的值是（ ）
如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD交于点P，则tan∠APC的值是（ ）| A． | $\frac{2}{3}$ | B． | 1 | C． | 2 | D． | $\frac{\sqrt{3}}{2}$ |