题目内容
17.下列图象可能是函数y=mx+n与y=mnx的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据m、n的取值,分别判断出两个函数图象所过的象限,要注意分类讨论.
解答 解:当mn>0,m,n同号,
同正时,y=mx+n过一、三、二象限;
同负时过二、四、三象限,
故D正确;
故选D.
点评 主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.

练习册系列答案
相关题目
7.如果向东走10米记作+10米,那么-5米表示( )
| A. | 向南走5米 | B. | 向西走-5米 | C. | 向西走5米 | D. | 向东走5米 |
8. 如图,点A、B、C都在⊙O上,若∠AOB+∠ACB=90°,则∠ACB的大小是( )
如图,点A、B、C都在⊙O上,若∠AOB+∠ACB=90°,则∠ACB的大小是( )
 如图,点A、B、C都在⊙O上,若∠AOB+∠ACB=90°,则∠ACB的大小是( )
如图,点A、B、C都在⊙O上,若∠AOB+∠ACB=90°,则∠ACB的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
12.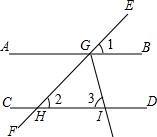 如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
 如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、G,已知∠1=∠2=40°,GI平分∠HGB交直线CD于点I,则∠3=( )| A. | 40° | B. | 50° | C. | 55° | D. | 70° |
9.下列方程中,有实数解的是( )
| A. | $\sqrt{x-1}$+4=0 | B. | $\sqrt{{x}^{2}+1}$=0 | C. | $\sqrt{2x+3}$=-x | D. | $\sqrt{2x-3}$+$\sqrt{x+3}$=0 |
6.计算:(-2)101+(-2)100的结果是( )
| A. | -2 | B. | -2100 | C. | 2 | D. | 2100 |
7.下列说法正确的是( )
| A. | 要了解一批灯泡的使用寿命,应采用普查的方式 | |
| B. | 若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖 | |
| C. | 了解无锡市每天的流动人口数,采用抽查方式 | |
| D. | “掷一枚硬币,正面朝上”是必然事件 |
 如图是由36个边长为1的正方形组成的6×6网格,则格点多边形ABCDE的面积是11.
如图是由36个边长为1的正方形组成的6×6网格,则格点多边形ABCDE的面积是11.