题目内容

3．如图所示，在△ABC中，∠A：∠B：∠BCA=1：2：3，CD⊥AB于D，AB=12，则DB等于（　　）
A．3B．4C．6D．9

分析 求出∠A=30°，在Rt△ACB中，根据直角三角形30°角所对的直角边等于斜边的一半求出BC，再在Rt△BDC中，根据直角三角形30°角所对的直角边等于斜边的一半求出DB即可得解．

解答 解：∵在△ABC中，∠A：∠B：∠BCA=1：2：3，
∴∠ACB=90°，∠A=30°，∠B=60°，
∵AB=12，
∴BC=6，
∵CD⊥AB，
∴∠BDC=90°，
∴∠BCD=30°，
∴BD=3．
故选A．

点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，熟记性质是解题的关键．

练习册系列答案
相关题目
13．方程2x2-4x+1=0化成（x+m）2=n（n≥0）的形式是（　　）
A．（x-1）2=$\frac{1}{2}$B．（2x-1）2=$\frac{1}{2}$C．（x-1）2=0D．（x-2）2=3
14．如图所示，AB是⊙O的弦，AB的长为24cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则OP的长的范围是（　　）
A．5≤OP≤12B．5≤OP≤10C．5≤OP≤13D．5≤OP≤24
11．已知三个数a、b、c的平均数是0，则这三个数在数轴上表示的位置不可能是（　　）
A．B．C．D．
18．根据下列条件判断△ABC的形状，并将题号填在横线上，①∠A=∠B=∠C；②∠A+∠B=∠C；③一个外角等于与它相邻的内角；④与∠A相邻的外角是60°；⑤∠A=32°，∠B=2∠C；⑥∠A=36°，∠B=3∠A；⑦∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C；⑧各内角都小于与它相邻的外角；⑨∠B=∠C=$\frac{1}{2}$∠A；⑩三角形的三个外角都相等．
其中，①⑩是等边三角形，①⑥⑨是等腰三角形，⑨是等腰直角三角形，②③⑦是直角三角形，①⑧⑩是锐角三角形，④⑤⑥是钝角三角形．
8．如图，点A、B、C都在⊙O上，若∠AOB+∠ACB=90°，则∠ACB的大小是（　　）
A．20°B．25°C．30°D．40°
15．下列说法正确的个数是（　　）
①位似图形一定是相似图形；
②相似图形一定是位似图形；
③两个位似图形的面积比等于位似比的平方；
④若五边形ABCDE与五边形A′B′C′D′E′位似，则其中△ABC与△A′B′C′也是位似图形，且位似比相等；
⑤两个位似图形上的对应线段必平行；
⑥位似图形上任意两点与位似中心的距离之比等于位似比．
A．1个B．2个C．3个D．4个
12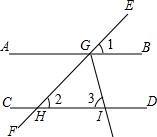．如图，直线EF分别与直线AB、CD相交于点G、G，已知∠1=∠2=40°，GI平分∠HGB交直线CD于点I，则∠3=（　　）
A．40°B．50°C．55°D．70°
13．三角形的一边长为3xcm，这条边上的高为xcm，其面积为ycm2，则y与x的函数关系是（　　）
A．y=x2B．y=2x2C．y=$\frac{1}{2}$x2D．y=$\frac{3}{2}$x2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网