题目内容
13．
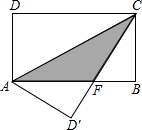如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
分析 因为BC为AF边上的高，要求△AFC的面积，求得AF即可，求证△AFD′≌△CFB，得BF=D′F，设D′F=x，则在Rt△AFD′中，根据勾股定理求x，于是得到AF=AB-BF，即可得到结果．
解答 解：易证△AFD′≌△CFB，
∴D′F=BF，
设D′F=x，则AF=8-x，
在Rt△AFD′中，（8-x）2=x2+42，
解之得：x=3，
∴AF=AB-FB=8-3=5，
∴S△AFC=$\frac{1}{2}$•AF•BC=10．
故选C．
点评 本题考查了翻折变换-折叠问题，勾股定理的正确运用，本题中设D′F=x，根据直角三角形AFD′中运用勾股定理求x是解题的关键．
练习册系列答案
相关题目
如图，把一张长方形纸条ABCD沿AF折叠，点B对应点E，已知∠ADB=20°，当AE∥BD时，∠BAF的度数为55°．
如图，扇形OAB是圆锥的侧面展开图，若OA=4$\sqrt{2}$cm，OA⊥OB，则这个圆锥的底面半径为$\sqrt{2}$cm．
如图，有以下四个条件：①∠B+∠BCD=180°，②∠1=∠2，③∠3=∠4，④∠B=∠5．其中不能判定AB∥CD的条件是（ ）
2．
如图，AB∥CD，点E在BC上，CD=CE，若∠ABC=34°，则∠BED的度数是（ ）
如图，AB∥CD，点E在BC上，CD=CE，若∠ABC=34°，则∠BED的度数是（ ）| A． | 104° | B． | 107° | C． | 116° | D． | 124° |