题目内容
1．计算或化简（1）-32+|-8|+（π-2015）0-（-$\frac{4}{3}$）-1
（2）（2a+3b）（3b-2a）
（3）19992（用乘法公式计算）
分析 （1）原式第一项利用乘方的意义计算，第二项利用绝对值的代数意义化简，第三项利用零指数幂法则计算，最后一项利用负整数指数幂法则计算即可得到结果；
（2）原式利用平方差公式化简即可；
（3）原式变形后，利用完全平方公式计算即可得到结果．
解答 解：（1）原式=-9+8+1+$\frac{3}{4}$=$\frac{3}{4}$；
（2）原式=9b2-4a2；
（3）原式=（2000-1）2=4000000-4000+1=3996001．
点评 此题考查了整式的混合运算，以及实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11．点P在第二象限，P到x轴的距离为4，P到y轴的距离为3，则点P纵坐标是（ ）
| A． | （4，3） | B． | （3，4） | C． | （-4，3） | D． | （-3，4） |
12．点（-2，5）关于x轴对称的点的坐标是（ ）
| A． | （2，-5） | B． | （-2，-5） | C． | （2，5） | D． | （5，-2） |
9．下列运算正确的是（ ）
| A． | a6÷a2=a4 | B． | a3+a3=a6 | C． | （-2x）3=-6x3 | D． | a3•a3=a9 |
16．弹簧挂上物体后会伸长（在允许挂物重量范围内），测得一弹簧的长度y（cm）与所挂的物体的重量x（kg）间有下表的关系：下列说法不正确的是（ ）
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A． | 弹簧不挂重物时的长度为8cm | |
| B． | x与y都是变量，且x是自变量，y是因变量 | |
| C． | 物体质量每增加1kg，弹簧长度y增加0.5cm | |
| D． | 所挂物体质量为7kg时，弹簧长度为13.5cm |
6．计算：（$\sqrt{3}$+$\sqrt{2}$）（$\sqrt{3}$-$\sqrt{2}$）=（ ）
| A． | 5+2$\sqrt{6}$ | B． | 1 | C． | 5-2$\sqrt{6}$ | D． | 5 |
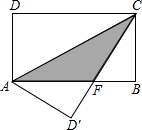如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（ ）
有若干张如图所示的正方形和长方形卡片，如果要拼一个长为（2a+b），宽为（a+b）的大长方形，那么需要A类卡片2张，B类卡片1张，C类卡片3张，请你在空白处画出一种拼法．