题目内容
8.如果$\frac{\sqrt{x-2}}{x-3}$有意义,那么x的取值范围是x≥2且x≠3.分析 根据二次根式的性质和分式的意义,即可求解.
解答 解:因为$\frac{\sqrt{x-2}}{x-3}$有意义,
可得:$\left\{\begin{array}{l}{x-2≥0}\\{x-3≠0}\end{array}\right.$,
解得:x≥2且x≠3.
故答案为:x≥2且x≠3
点评 主要考查了二次根式的意义和分式的性质.二次根式中的被开方数必须是非负数,否则二次根式无意义.当二次根式在分母上时还要考虑分母不等于零,此时被开方数大于0.

练习册系列答案
相关题目
19.某市5月上旬前5天的最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法正确的是( )
| A. | 极差是3 | B. | 极差是5 | C. | 极差是7 | D. | 极差是9 |
16.弹簧挂上物体后会伸长(在允许挂物重量范围内),测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | 弹簧不挂重物时的长度为8cm | |
| B. | x与y都是变量,且x是自变量,y是因变量 | |
| C. | 物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 所挂物体质量为7kg时,弹簧长度为13.5cm |
3.已知点M(-2,3)在双曲线y=$\frac{k}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (3,2) | B. | (-2,-3) | C. | (2,3) | D. | (3,-2) |
18.下列多项式中,在有理数范围内不能用平方差公式分解因式的是( )
| A. | -x2+y2 | B. | 4a2-(a+b)2 | C. | -a2-9b2 | D. | x2y2-1 |
 如图,在△ABC中,AD⊥BC于D,EF⊥BC于F,BE交AD于G,EF是∠BEC的角平分线,证明:∠EAG=∠AGE.
如图,在△ABC中,AD⊥BC于D,EF⊥BC于F,BE交AD于G,EF是∠BEC的角平分线,证明:∠EAG=∠AGE.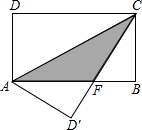 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( ) 如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD.