题目内容
3.解方程组①$\left\{\begin{array}{l}{x-2y=3}\\{3x-8y=13}\end{array}$
②$\left\{\begin{array}{l}{x+y=300}\\{5%x+53%y=25%×300}\end{array}$.
分析 ①方程组利用加减消元法求出解即可;
②方程组整理后,利用加减消元法求出解即可.
解答 解:①$\left\{\begin{array}{l}{x-2y=3①}\\{3x-8y=13②}\end{array}\right.$,
①×3-②得:2y=-4,即y=-2,
把y=-2代入①得:x=-1,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$;
②方程组整理得:$\left\{\begin{array}{l}{x+y=300①}\\{5x+53y=7500②}\end{array}\right.$,
②-①×5得:48y=6000,即y=125,
把y=125代入①得:x=175,
则方程组的解为$\left\{\begin{array}{l}{x=175}\\{y=125}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
18.下列多项式中,在有理数范围内不能用平方差公式分解因式的是( )
| A. | -x2+y2 | B. | 4a2-(a+b)2 | C. | -a2-9b2 | D. | x2y2-1 |
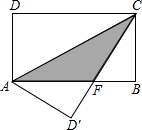 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( ) 有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2a+b),宽为(a+b)的大长方形,那么需要A类卡片2张,B类卡片1张,C类卡片3张,请你在空白处画出一种拼法.
有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2a+b),宽为(a+b)的大长方形,那么需要A类卡片2张,B类卡片1张,C类卡片3张,请你在空白处画出一种拼法.