题目内容
18. 如图,扇形OAB是圆锥的侧面展开图,若OA=4$\sqrt{2}$cm,OA⊥OB,则这个圆锥的底面半径为$\sqrt{2}$cm.
如图,扇形OAB是圆锥的侧面展开图,若OA=4$\sqrt{2}$cm,OA⊥OB,则这个圆锥的底面半径为$\sqrt{2}$cm.
分析 把扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
解答 解:设此圆锥的底面半径为r,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
2πr=$\frac{90π×4\sqrt{2}}{180}$,
r=$\sqrt{2}$cm.
故答案为$\sqrt{2}$cm.
点评 主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
9.下列运算正确的是( )
| A. | a6÷a2=a4 | B. | a3+a3=a6 | C. | (-2x)3=-6x3 | D. | a3•a3=a9 |
6.计算:($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=( )
| A. | 5+2$\sqrt{6}$ | B. | 1 | C. | 5-2$\sqrt{6}$ | D. | 5 |
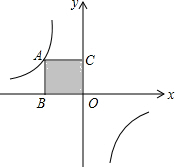 如图,正方形ABOC的面积为4,反比例函数y=$\frac{k}{x}$的图象过点A,则k=-4.
如图,正方形ABOC的面积为4,反比例函数y=$\frac{k}{x}$的图象过点A,则k=-4.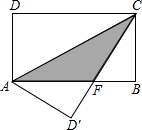 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )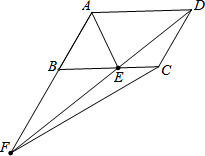 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
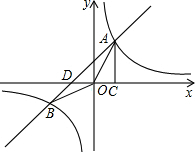 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,