题目内容
15.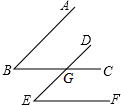 已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.
已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.
分析 (1)先由两直线平行同位角相等,得到两对角相等,再等量代换即可得证;
(2)分两种情况:①由已知AB∥EF,BC∥DE,根据平行线的性质得:∠3=∠1,∠3=∠2⇒∠1=∠2;②由已知AB∥EF,BC∥DE,得:∠3+∠1=180°,∠3=∠2⇒∠1+∠2=180°.据此得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
解答  解:(1)∠B=∠E,
解:(1)∠B=∠E,
理由为:如图,∵AB∥DE,BC∥EF,
∴∠B=∠DGC,∠DGC=∠E,
∴∠B=∠E.
(2)①如图,AB∥EF,BC∥DE,则∠1与∠2的数量关系是:相等.
理由是:∵BC∥DE,
∴∠1=∠AGD.
∵AB∥EF,
∴∠2=∠AGD,
∴∠1=∠2;
②如图2,AB∥EF,BC∥DE,则∠1与∠2的数量关系是:互补.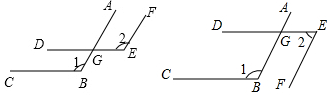
理由是:∵BC∥DE,
∴∠1=∠EGB.
∵AB∥EF,
∴∠2+∠EGB=180°,
∴∠1+∠2=180°,
即∠1与∠2互补.
综上所述,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案是:相等或互补.
点评 此题主要考查了平行线的性质,熟练掌握平行线的性质是解本题的关键,解题时注意分类思想的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )
 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | AB=CD | D. | ∠BAD=∠BCD |
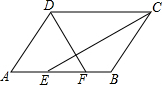 如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.
如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.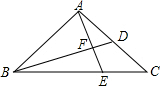 如图,在△ABC中,BD是AC边上的中线,E是BC上一点,AE与BD相交于点F.
如图,在△ABC中,BD是AC边上的中线,E是BC上一点,AE与BD相交于点F.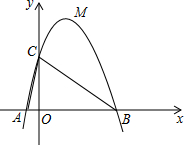 如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1
如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1

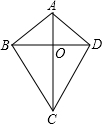 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )