题目内容
6.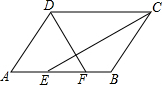 如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.
如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.(1)若AB=5,BC=3,求EF的长;
(2)若BC=3,EF=1,求AB的长;
(3)若BC=a,AB=b,且a<b,求点E、F之间的距离.(用含a、b的代数式表示)
分析 (1)根据角平分线的定义以及平行线的性质,得出∠AFD=∠ADF,进而得到AF=AD=BC=3,同理可得,BE=CB=3,最后根据EF=BE+AF-AB进行计算即可;
(2)根据角平分线的定义以及平行线的性质,得出∠BCE=∠BEC,进而得到BC=BE=3,再根据EF=1,求得BF=3-1=2,同理可得,AD=AF=3,最后根据AB=AF+BF进行计算即可;
(3)根据角平分线的定义以及平行线的性质,∠AFD=∠ADF,进而得出AF=AD=BC=a,同理可得,BE=CB=a,得出AE=AB-BE=b-a,最后得到EF=|AF-AE|=|a-b+a|=|2a-b|.
解答  解:(1)∵DF平分∠ADC,
解:(1)∵DF平分∠ADC,
∴∠ADF=∠CDF,
又∵AB∥CD,
∴∠AFD=∠CDF,
∴∠AFD=∠ADF,
∴AF=AD=BC=3,
同理可得,BE=CB=3,
∴EF=BE+AF-AB=3+3-5=1;
(2)∵CE平分∠DCB,
∴∠DCE=∠BCE,
又∵AB∥CD,
∴∠DCE=∠BEC,
∴∠BCE=∠BEC,
∴BC=BE=3,
∵EF=1,
∴BF=3-1=2,
同理可得,AD=AF=3,
∴AB=AF+BF=3+2=5;
(3)∵DF平分∠ADC,
∴∠ADF=∠CDF,
又∵AB∥CD,
∴∠AFD=∠CDF,
∴∠AFD=∠ADF,
∴AF=AD=BC=a,
同理可得,BE=CB=a,
∴AE=AB-BE=b-a,
∴EF=|AF-AE|=|a-b+a|=|2a-b|.
点评 此题主要考查了角平分线的定义、平行四边形的性质、平行线的性质等知识的综合应用,解决问题的关键是找出线段之间的关系:EF=BE+CF-BC.

练习册系列答案
相关题目
16.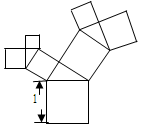 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )
有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )
 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )
有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )| A. | 1 | B. | 2015 | C. | 2016 | D. | 2017 |
11.点P(-3,5)关于y轴的对称点P'的坐标是( )
| A. | (3,5) | B. | (5,-3) | C. | (3,-5) | D. | (-3,-5) |
18.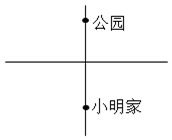 如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
 如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 0 |
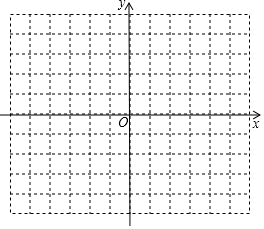 如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).
如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).



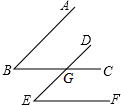 已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.
已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补. 如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.
如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.