题目内容
19.已知抛物线的顶点为(-1,4),且在x轴上截得的弦长为6,求抛物线的解析式.分析 设此抛物线的解析式为:y=a(x-h)2+k,由已知条件可得h=-1,k=4,再有条件:它在x轴上截得的线段长为6,求出a的值即可.
解答 解:设此抛物线的解析式为:y=a(x-h)2+k,
∵抛物线的顶点坐标为(-1,4),
∴,
∴y=a(x+1)2+4,
∵且它在x轴上截得的线段长为6,
令y=0得,方程0=a(x+1)2+4,
即:ax2+2ax+a+4=0,
∵抛物线y=a(x+1)2+4在x轴上的交点的横坐标为方程的根,设为x1,x2,
∴x1+x2=2,x1•x2=$\frac{a+4}{a}$,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=6,
即4-4×$\frac{a+4}{a}$=36
解得:a=-$\frac{4}{9}$,
∴该抛物线的解析式为:y=-$\frac{4}{9}$(x+1)2+4.
点评 此题主要考查了用顶点式求二次函数的解析式和一元二次方程与二次函数的关系,函数与x轴的交点的横坐标就是方程的根.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,将纸片沿虚线拆叠可得一个正方形,则和平面A相对的面是E.
如图,将纸片沿虚线拆叠可得一个正方形,则和平面A相对的面是E. 已知:如图,∠1和线段m.
已知:如图,∠1和线段m. 如图是单位长度为1的网格,在图中画一个格点三角形ABC,使其周长等于7+$\sqrt{13}$.
如图是单位长度为1的网格,在图中画一个格点三角形ABC,使其周长等于7+$\sqrt{13}$. 如图,在Rt△ABC和Rt△BAD中,∠C=∠D=90°,AD平分∠CAB,BC平分∠ABD,AD、BC相交于点O,求证:OC=OD.
如图,在Rt△ABC和Rt△BAD中,∠C=∠D=90°,AD平分∠CAB,BC平分∠ABD,AD、BC相交于点O,求证:OC=OD.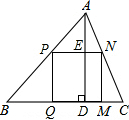 △ABC是一块钝角三角形的余料,如图所示,BC=48cm,高AD=16cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,求这个正方形零件的边长是多少?
△ABC是一块钝角三角形的余料,如图所示,BC=48cm,高AD=16cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,求这个正方形零件的边长是多少? 已知:如图,正方形ABCD和正三角形ADE,求证:△BCE是等腰三角形.
已知:如图,正方形ABCD和正三角形ADE,求证:△BCE是等腰三角形.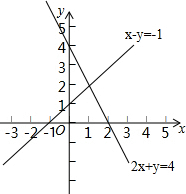 直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.