题目内容
9．
如图，方格纸中每个小方格的边长为1，画一条长为$\sqrt{18}$的线段．
分析 根据勾股定理，可知两直角边都是3的等腰直角三角形的斜边长为$\sqrt{18}$．
解答 解：如图，等腰直角三角形ABC中，∠ACB=90°，AC=BC=3，
那么AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=$\sqrt{18}$，
即线段AB是所求作的线段．
点评 本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．即如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
小学期末标准试卷系列答案
相关题目
如图，Rt△ABC中，BC=11cm，AC=7cm，点M从点B出发沿BC匀速向点C运动，点N从点C出发沿CA匀速向点A运动．
如图，△ABC与△DEF是中心对称图形，A，B，C的对应点分别是D，E，F，小明画好点D后有事走开了，请你帮他把△DEF画完整．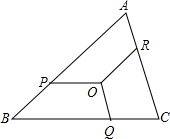
如图，点O是△ABC内一点，点P、Q、R分别在边AB、BC、CA上，且OP∥BC，OQ∥CA，OR∥AB，OP=OQ=OR，BC=a，CA=b，AB=c，求OP的长．
如图是单位长度为1的网格，在图中画一个格点三角形ABC，使其周长等于7+$\sqrt{13}$．
如图，△ABC中，AB=AC，∠BAC=90°，点D是BC的中点，点M是BD上一点，过C作CN⊥AM于N，交AD于E，求证：BM=AE．
如图，C为BE上一点，AB=AC，BE=CD．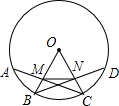
如图，在⊙O中，$\widehat{AB}=\widehat{BC}=\widehat{CD}$，半径OB，OC分别交弦AC，BD于点M，N，求证：∠OMN=∠ONM．