题目内容
15. 根据下列证明过程填空:
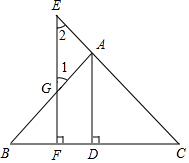
根据下列证明过程填空:已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD (平面内,垂直于同一条直线的两直线平行 ),
∴∠1=∠DAB ( 两直线平行,内错角相等 ),
∠E=∠CAD (两直线平行,同位角相等 ).
∵∠1=∠2 (已知),
∴∠BAD=∠CAD,即AD平分∠BAC (角平分线定义).
分析 根据等腰三角形的性质得出∠E=∠AGE,根据AD⊥BC,EF⊥BC推出AD∥EF,根据平行线的性质得出∠AGE=∠DAB,∠E=∠DAC,推出∠DAB=∠DAC即可.
解答 证明:∵AD⊥BC,EF⊥BC,
∴∠ADC=∠EFC=90°,
∴AD∥EF,(平面内,垂直于同一条直线的两直线平行)
∴∠AGE=∠DAB,∠E=∠DAC,
∵AE=AG,
∴∠E=∠AGE,
∴∠DAB=∠DAC,
即AD平分∠BAC.
故答案为:平面内,垂直于同一条直线的两直线平行,∠1,∠BAD,∠2,两直线平行,同位角相等,∠1=∠2,∠BAD=∠CAD,角平分线定义.
点评 本题考查了等腰三角形的性质,垂直定义,平行线的性质和判定,主要考查学生的推理能力.

练习册系列答案
相关题目
5.小明同学平时爱好数学,他探索发现了:从2开始,连续的几个偶数相加,它们和的情况变化规律,如表所示:
请你根据表中提供的规律解答下列问题:
(1)如果n=8时,那么S的值为72;
(2)根据表中的规律猜想:用n的代数式表示S,则S=2+4+6+8+…+2n=n(n+1);
(3)利用上题的猜想结果,计算100+102+104+…+1010+1012的值(要有计算过程).
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(1)如果n=8时,那么S的值为72;
(2)根据表中的规律猜想:用n的代数式表示S,则S=2+4+6+8+…+2n=n(n+1);
(3)利用上题的猜想结果,计算100+102+104+…+1010+1012的值(要有计算过程).
 如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不计螺丝大小,其中相邻两螺丝的距离依次为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不计螺丝大小,其中相邻两螺丝的距离依次为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( ) 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )