题目内容

3．如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC于点D，CD=3，则BC的长为（　　）
A．6B．9C．10D．12

分析 根据三角形内角和定理求出∠BAC，根据线段垂直平分线的性质得到AD=BD，求出∠BAD和∠CAD，根据直角三角形的性质解答即可．

解答 解：∵∠C=90°，∠B=30°，
∴∠BAC=60°，
∵DE是AB的垂直平分线，
∴DB=DA，
∴∠BAD=∠B=30°，
∴∠CAD=30°，
∴AD=2CD=6，
∴DB=AD=6，
∴BC=3+6=9，
故选：B．

点评 本题考查的是直角三角形的性质、线段垂直平分线的性质，掌握线段垂直平分线上任意一点，到线段两端点的距离相等是解题的关键．

练习册系列答案
相关题目

我国古代名著《九章算术》中有一题“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”（凫：野鸭）设野鸭与大雁从北海和南海同时起飞，经过x天相遇，可列方程为（　 　）

A. （9﹣7）x=1 B. （9+7）x=1 C. D.

14．化简求值：
①5（3a2b-ab2）-2（ab2+3a2b），其中 a=-2，b=-1．
②2m-{7n+[4m-7n-2（m-2n-3m）]-3m}，其中m=-3，n=2．
11．如图，在平面直角坐标系中，点A在第一象限，且OA=6，与x轴相切于点B，
且∠AOB=30°
（1）求⊙A的半径长；
（2）将沿x轴方向平移（3$\sqrt{3}$±3）个单位长度与y轴相切．
18．有理数a，b，c在数轴上的位置如图所示．
（1）用“＜”连接：0，a，b，c；
（2）化简代数式：3|c-a|+2|b-c|-3|a+b|．
8．在△ABC中，∠A=50°，∠B=80°，则△ABC是（　　）
A．钝角三角形B．等腰三角形C．等边三角形D．等腰直角三角形
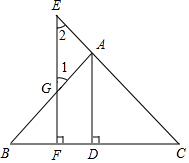15．根据下列证明过程填空：
已知：如 图，AD⊥BC于点D，EF⊥BC于点F，交AB于点G，交CA的延长线于点E，∠1=∠2．
求证：AD平分∠BAC，填写证明中的空白．
证明：
∵AD⊥BC，EF⊥BC  （已知），
∴EF∥AD   （平面内，垂直于同一条直线的两直线平行 ），
∴∠1=∠DAB （  两直线平行，内错角相等 ），
∠E=∠CAD   （两直线平行，同位角相等 ）．
∵∠1=∠2 （已知），
∴∠BAD=∠CAD，即AD平分∠BAC  （角平分线定义）．
12．在等腰Rt△ABC中，∠ACB=90°，AC=BC，点D是BC边上一点，BN⊥AD交AD的延长线于点N．

（1）如图1，若CM∥BN交AD于点M．
①直接写出图1中所有与∠MCD相等的角：∠CAD，∠CBN；（注：所找到的相等关系可以直接用于第②小题的证明过程
②过点C作CG⊥BN，交BN的延长线于点G，请先在图1中画出辅助线，再回答线段AM、CG、BN有怎样的数量关系，并给予证明．
（2）如图2，若CM∥AB交BN的延长线于点M．请证明：∠MDN+2∠BDN=180°．
13．有理数的计算
（1）-14-|-7|+3-2×（-1$\frac{1}{2}$）；             
（2）1.25×（-4）-32×（$\frac{3}{8}$-$\frac{1}{4}$-$\frac{15}{16}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网