题目内容
19.如图,已知正方形ABCD,直线AB绕点A顺时针旋转α角(0°<α<180°),得直线AP,点B关于直线AP的对称点为E,连接AE,BE,DE,其中DE交直线AP于点F.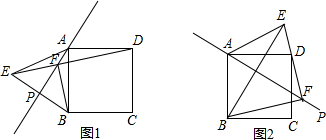
(1)如图1,当α=20°,∠ADF的度数为25°;当0°<α<45°时,△BEF的形状是等腰直角三角形;
(2)如图2,当90°<α<180°时,猜测线段AB,EF,DF之间的数量关系,并证明你的结论;
(3)若正方形ABCD的边长为6,当α=30°时,DE的长为$3\sqrt{6}+3\sqrt{2}$;当α=120°时,DE的长为$3\sqrt{6}-3\sqrt{2}$.
分析 (1)利用轴对称的性质以及等腰三角形的性质得出即可;
(2)由轴对称的性质可得:EF=BF,AE=AB=AD,∠ABF=∠AEF=∠ADF,进而利用勾股定理得出答案;
(3)根据α=30°,α=120°两种情况进行解答即可.
解答 解:(1)当α=20°,则∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAD=130°,
∴∠ADF=25°,
∵点B关于直线AP的对称点为E,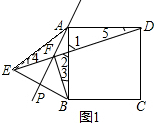
∴EF=BF,AE=AB,
∴△AEF和△ABF关于直线AP对称,
∴∠3=∠4,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴AE=AD,∠1+∠5=90°,
∴∠4=∠5,
∴∠3=∠5,
∵∠1=∠2,
∴∠2+∠3=∠1+∠5=90°,
∴∠BFD=90°,
∴BF⊥ED,
∵AE=AB,
∴△BEF是等腰直角三角形;
(2)BF2+FD2=2AB2.
理由:如图2,
连接BD,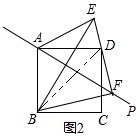
由轴对称的性质可得:EF=BF,AE=AB=AD,∠ABF=∠AEF=∠ADF,
则∠BFD=∠BAD=90°,
故BF2+FD2=BD2,
则BF2+FD2=2AB2.
(3)正方形ABCD的边长为6,当α=30°时,DE=$3\sqrt{6}+3\sqrt{2}$;当α=120°时,DE=$3\sqrt{6}-3\sqrt{2}$.
点评 本题考查了正方形的性质、轴对称的性质、旋转的性质以及等腰三角形的判定与性质、面积的计算方法;熟练掌握正方形和轴对称的性质得出等腰三角形,进一步得出角之间的关系是解决问题的关键.

练习册系列答案
相关题目
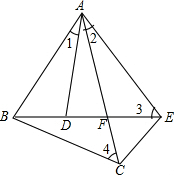 如图,已知∠1=∠2,∠3=∠4,求证:△ABD∽△ACE.
如图,已知∠1=∠2,∠3=∠4,求证:△ABD∽△ACE.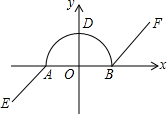 如图,在平面直角坐标系中,我们把由两条射线AE、BF和以AB为直径的半圆的组成的图形叫做π图形(注:不含线段AB),已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
如图,在平面直角坐标系中,我们把由两条射线AE、BF和以AB为直径的半圆的组成的图形叫做π图形(注:不含线段AB),已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上. 如图,AB是⊙O的直径,BC是⊙O切线,切点为B,OC平行于弦AD,OA=2.
如图,AB是⊙O的直径,BC是⊙O切线,切点为B,OC平行于弦AD,OA=2.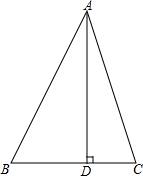 如图,△ABC中,∠A=45°,过点A作AD⊥BC,BD=2,BC=3,求S△ABC.
如图,△ABC中,∠A=45°,过点A作AD⊥BC,BD=2,BC=3,求S△ABC.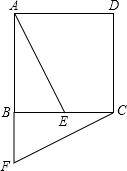 如图,正方形ABCD中,E为BC边上的一点,将△ABE旋转后得到△CBF.
如图,正方形ABCD中,E为BC边上的一点,将△ABE旋转后得到△CBF.