题目内容
10.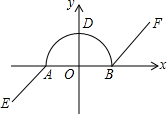 如图,在平面直角坐标系中,我们把由两条射线AE、BF和以AB为直径的半圆的组成的图形叫做π图形(注:不含线段AB),已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
如图,在平面直角坐标系中,我们把由两条射线AE、BF和以AB为直径的半圆的组成的图形叫做π图形(注:不含线段AB),已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.(1)连接AD、BD,求两条射线AE、BF所在直线的距离;
(2)当一次函数y=x+b的图象与π形图恰好只有一个公共点时,直接写出b的取值范围.
分析 (1)利用直径所对的圆周角是直角,从而判定三角形ADB为等腰直角三角形,其直角边的长等于两直线间的距离;
(2)利用数形结合的方法得到当直线与π形图有一个交点时自变量x的取值范围即可.
解答 解:(1)如图,分别连接AD、DB,则点D在直线AE上,
∵点D在以AB为直径的半圆上,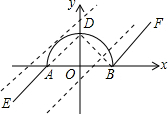
∴∠ADB=90°,
∴BD⊥AD,
在Rt△DOB中,由勾股定理得,BD=$\sqrt{2}$,
∵AE∥BF,
∴两条射线AE、BF所在直线的距离为$\sqrt{2}$.
(2)当一次函数y=x+b的图象与π形图恰好只有一个公共点时,b的取值范围是b=$\sqrt{2}$或-1<b<1.
点评 本题考查了一次函数的性质,还涉及到了勾股定理及圆周角定理的相关知识,熟练掌握一次函数的性质是解题的关键.

练习册系列答案
相关题目
5.反比例函数y=$\frac{1-2m}{x}$中,当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m<2 | C. | m<$\frac{1}{2}$ | D. | m>2 |
 在数轴上表示-2$\frac{2}{3}$,3,0及它们的相反数,并回答数轴上表示互为相反数的两个点和原点有什么关系?
在数轴上表示-2$\frac{2}{3}$,3,0及它们的相反数,并回答数轴上表示互为相反数的两个点和原点有什么关系?
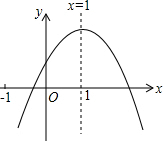 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: