题目内容
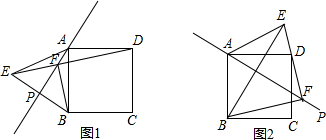
8.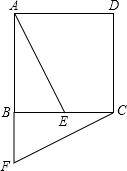 如图,正方形ABCD中,E为BC边上的一点,将△ABE旋转后得到△CBF.
如图,正方形ABCD中,E为BC边上的一点,将△ABE旋转后得到△CBF.(1)旋转中心是点B;旋转角度是90°.
(2)如果正方形的面积是18cm2,△BCF的面积是5cm2,则四边形ABCD的面积是多少?
分析 (1)利用正方形的性质得BA=BC,∠ABC=90°,然后根据旋转的性质可判断旋转中心为点B,旋转角为90°;
(2)根据旋转的性质得S△ABE=S△BCF=5,然后利用四边形AECD的面积=S正方形ABCD-S△ABE进行计算即可.
解答 解:(1)∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∵将△ABE旋转后得到△CBF,
∴旋转中心为点B,∠ABC等于旋转角,即旋转角为90°;
故答案为点B,90°;
(2)∵△ABE旋转后得到△CBF,
∴S△ABE=S△BCF=5,
∴四边形AECD的面积=S正方形ABCD-S△ABE
=18-5
=13(cm2).
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
相关题目
16.已知两圆的圆心距为5,两圆的半径分别是方程x2-6x+5=0的两根,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
3.哈尔滨市地域广阔,总面积为53 200平方公里,这个数用科学记数法表示为( )
| A. | 5.32×104 | B. | 5.32×103 | C. | 5.32×102 | D. | 53.2×104 |
13.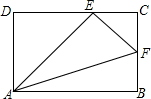 如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
 如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )| A. | △ABF∽△AEF | B. | △ABF∽△CEF | C. | △CEF∽△DAE | D. | △DAE∽△BAF |
18.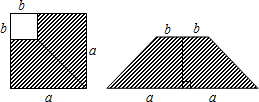 如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )
如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )
 如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )
如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )| A. | (a-b)2=a2-2ab+b2 | B. | (a+b)2=a2+2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | a(a-b)=a2-ab |
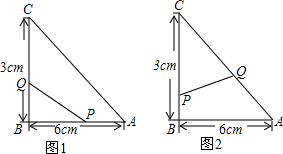
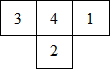 如图所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
如图所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.