题目内容
1.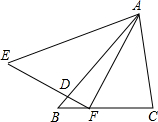 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
| A. | 只有①③ | B. | 只有①④ | C. | 只有③④ | D. | 只有①③④ |
分析 根据SAS推出△AEF≌△ABC,推出AF=AC,根据等边对等角推出即可;根据已知条件即可判断②,根据∠E=∠B,∠EDA=∠BDF,推出△ADE∽△FBD即可;根据全等三角形性质得出∠EAF=∠BAC,求出∠EAD=∠CAF,根据相似三角形性质得出∠BFD=∠EAD=∠CAF,即可判断④,即可得出选项.
解答 解:在△AEF和△ABC中
$\left\{\begin{array}{l}{AE=AB}\\{∠E=∠B}\\{EF=BC}\end{array}\right.$,
∴△AEF≌△ABC(SAS),
∴AF=AC,
∴∠AFC=∠C,∴①正确;
根据已知条件不能推出DF=CF,∴②错误;
∵∠E=∠B,∠EDA=∠BDF,
∴△ADE∽△FBD,∴③正确;
∵△AEF≌△ABC,
∴∠EAF=∠BAC,
∴∠EAF-∠DAF=∠BAC-∠DAF,
∴∠EAD=∠CAF,
∵△ADE∽△FBD,
∴∠BFD=∠EAD=∠CAF,∴④正确;
故选D.
点评 本题考查了等腰三角形的性质和判定,相似三角形的性质和判定,全等三角形的性质和判定等知识点的综合运用,主要考查学生的推理能力和辨析能力,题目比较典型,但是有一定的难度.

练习册系列答案
相关题目
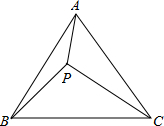 已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.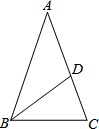 如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).
如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).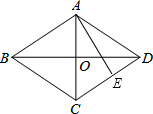 如图,菱形花坛ABCD的边长为20m,DE=CE,AE⊥CD,沿对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
如图,菱形花坛ABCD的边长为20m,DE=CE,AE⊥CD,沿对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积. 如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,BC′交AD于E.
如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,BC′交AD于E.