题目内容
19.若-2≤x≤0,求y=2x2-x+1的最大值、最小值.分析 求出顶点坐标,再求出x=0,x=-2时的y的值,然后作出判断.
解答 解:当x=-2时,y=11,
当x=0时,y=1,
又∵y=2x2-x+1=2(x-$\frac{1}{4}$)2+$\frac{7}{8}$.
∴x=$\frac{1}{4}$时,y最小值=$\frac{7}{8}$,
综上所述若-2≤x≤0时,y=2x2-x+1的最大值是11、最小值是1.
点评 本题考查二次函数的最值问题,需要熟练掌握配方法求顶点坐标,会判断最值问题,注意自变量x在端点时函数值y的取值,属于中考常考题型.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
14.一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
| A. | 第一次向右拐40°,第二次向左拐40° | |
| B. | 第一次向右拐50°,第二次向左拐130° | |
| C. | 第一次向右拐50°,第二次向右拐130° | |
| D. | 第一次向左拐50°,第二次向左拐130° |
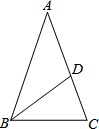 如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).
如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一). 如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,BC′交AD于E.
如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,BC′交AD于E. 如图,直线l1∥l2,∠α=∠β,∠1=35°,则∠2=145°.
如图,直线l1∥l2,∠α=∠β,∠1=35°,则∠2=145°.