题目内容
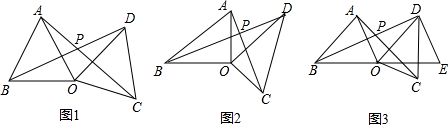
13.已知:△CDO≌△ABO,其中C与A,D与B对应,在△CDO绕点O旋转过程中,连接AC和BD,设直线AC与BD的交点为P.(1)如图1,若△ABO是等边三角形,请探究并猜想:
线段AC与BD的数量关系为AC=BD,∠APB的度数为60°;
(2)如图2,若△ABO是直角三角形,且∠AOB=90°,OA=2,OB=3,设线段AC=kBD,求证:AC⊥BD,并求出k的值;
(3)如图3,若△ABO是锐角三角形,且∠AOB=65°,OA=2,OB=3,延长BO至点E,使OE=OB,连接DE,设线段AC=kBD.
①直接写出k的值和∠APB的度数;
②求AC2+(kDE)2的值.
分析 (1)根据全等三角形的性质得到AO=BO=OD=OC,∠AOB=∠COD=60°,根据全等三角形的性质得到∠OAC=∠OBD,推出A,B,O,D四点共圆,根据圆周角定理即可得到结论;
(2)根据全等三角形的性质得到OC=OA,OD=OB,∠AOB=∠COD,由相似三角形的性质得到∠OAC=∠OBD根据余角的性质得到AD⊥BD根据相似三角形的性质得到k=$\frac{2}{3}$;
(3)①根据全等三角形的性质得到OC=OA,OD=OB,∠AOB=∠COD,根据相似三角形的性质得到k=$\frac{2}{3}$;②由已知得到O是BE的中点,根据全等三角形的性质得到OD=OB=$\frac{1}{2}$BE,由圆周角定理得到∠BDE=90°根据勾股定理即可得到结论.
解答 解:(1)∵△CDO≌△ABO,△ABO是等边三角形,
∴AO=BO=OD=OC,∠AOB=∠COD=60°,
∴∠AOC=∠BOD,
在△AOC与△BOD中,$\left\{\begin{array}{l}{AO=BO}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD,∠OAC=∠OBD,
∴A,B,O,D四点共圆,
∴∠APB=∠AOB=60°,
故答案为:AC=BD,60°;
(2)∵△CDO≌△ABO,
∴OC=OA,OD=OB,∠AOB=∠COD,
∴∠AOC=∠BOD,
∴$\frac{OC}{OD}=\frac{OA}{OB}$,
∴△AOC∽△BOD,
∴∠OAC=∠OBD,
∵∠AOB=90°,
∴∠OBD+∠ABP+∠OAB=90°,
∴∠OAC+∠ABP+∠OAB=90°,
∴∠APB=90°,
∴AD⊥BD,
∵△AOC∽△BOD,
∴$\frac{AC}{BD}=\frac{OA}{OB}=\frac{2}{3}$,
∵AC=kBD,
∴k=$\frac{2}{3}$;
(3)①∵△CDO≌△ABO,
∴OC=OA,OD=OB,∠AOB=∠COD,
∴∠AOC=∠BOD,
∴$\frac{OC}{OD}=\frac{OA}{OB}$,
∴△AOC∽△BOD,
∴∠OAC=∠OBD,
∴A,B,O,D四点共圆,
∴∠APB=∠AOB=65°,
∵△AOC∽△BOD,
∴$\frac{AC}{BD}=\frac{OA}{OB}=\frac{2}{3}$,
∵AC=kBD,
∴k=$\frac{2}{3}$;
②∵延长BO至点E,使OE=OB,
∴O是BE的中点,
∵△CDO≌△ABO,
∴OD=OB=$\frac{1}{2}$BE,
∴点D在以O为圆心,BE为直径的圆上,
∴∠BDE=90°,
∴BD2+DE2=BE2=62=36,
∴AC2+(kDE)2=(kBD)2+(kDE)2=k2(BD2+DE2)=($\frac{2}{3}$)2×36=16.
点评 本题考查了全等三角形的性质和判定,相似三角形的判定和性质,勾股定理,四点共圆,圆周角定理,等边三角形的性质,熟练掌握相似三角形的判定定理是解题的关键.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| A. | 第一次向右拐40°,第二次向左拐40° | |
| B. | 第一次向右拐50°,第二次向左拐130° | |
| C. | 第一次向右拐50°,第二次向右拐130° | |
| D. | 第一次向左拐50°,第二次向左拐130° |
 某市为了迎接新年搞大型庆典活动,在庆典中心竖起(与地面垂直)一个高为4.4米的抛物线形彩虹门(门的厚度不计),如果以过彩门的两个着地点所在直线为x轴,以过门的最高点且垂直地面的直线为y轴建立直角坐标系,则彩虹门可以近似地看成抛物线y=-1.1x2+4.4的一部分,
某市为了迎接新年搞大型庆典活动,在庆典中心竖起(与地面垂直)一个高为4.4米的抛物线形彩虹门(门的厚度不计),如果以过彩门的两个着地点所在直线为x轴,以过门的最高点且垂直地面的直线为y轴建立直角坐标系,则彩虹门可以近似地看成抛物线y=-1.1x2+4.4的一部分, 如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.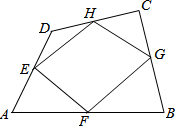 如图,E、F、G、H分别是凸四边形ABCD的四边的中点,顺次连接E、F、G、H这四点围成四边形EFGH.
如图,E、F、G、H分别是凸四边形ABCD的四边的中点,顺次连接E、F、G、H这四点围成四边形EFGH.