题目内容
4．如图（1）、（2）、（3）所示，每个图形分别有3、6、9个三角形；若在BC上有n个点，则应有$\frac{1}{2}$（n+1）（n+2）个三角形．
分析 图1中的三角形有：△ABD1、△ABC、△AD1 C 三个；图2中三角形有：△ABD1、△ABD2、△ABC、△AD1 D2、△AD1 C、△AD2 C，如此分析当BC上的点的个数分别是1、2、3…n时三角形的个数随点数的变化规律即可．
解答 解：当BC上的点的个数分别是1时，三角形的个数为：2+1=3（个）；当BC上的点的个数分别是2时，三角形的个数为：3+2+1=6（个）；当BC上的点的个数分别是3时，三角形的个数为：4+3+2+1=10（个）…当BC上的点的个数分别是n时，三角形的个数随点数为：（n+1）+n+…+3+2+1=$\frac{1}{2}$（n+1）（n+2）．
故答案为：3；6；9；$\frac{1}{2}$（n+1）（n+2）
点评 本题考查了图形的变化规律问题解题的关键是找到当BC上的点的个数分别是1、2、3…n时三角形的个数随点数的变化规律．
练习册系列答案
相关题目
探索与发现
如图，位于A处的海上救援中心获悉：在其北偏东68°方向的B处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船，此时，遇险船在救生船的正东方向B处，现救生船沿着航线CB前往B处救援，求救生船到达B处行驶的距离？（参考数据：sin68°≈0.90，cos68°≈0.36，tan68°≈2.50，$\sqrt{3}$≈1.7）
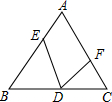如图，在等边三角形△ABC中，点D为线段BC的中点，点E、F分别在线段AB和AC上，∠EDF=60°．