Question

14．在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A′B′C′．
（1）如图（1），当旋转角θ为多少度时，AB∥CB′？
（2）在（1）的条件下，设A′B′与CB相交于点D．试判断△A′CD的形状，并说明理由；
（3）如图（2），设AC中点为E，A′B′中点为P，AC=a，连接EP，当θ=120°时，EP长度最大，最大值为$\frac{3}{2}$a．

Answer 1

分析 （1）求出∠BCB′=∠B=30°，根据平行线的判定得出即可；
（2）求出∠A′=∠ACD=60°，根据等边三角形的判定得出即可；
（3）连结CP，如图1，利用含30度的直角三角形三边的关系得AB=2AC=2a，由E为AC的中点得CE=$\frac{1}{2}$a，再根据旋转的性质得A′B′=AB=2a，则根据直角三角形斜边上的中线性质易得CP=$\frac{1}{2}$A′B′=a，于是根据三角形三边的关系有PE＜CE+PC，所以只有当点P在EC的延长线上时，PE最大，此时PE=CE+PC=$\frac{3}{2}$a，如图2．

解答 解：（1）当θ=30°时，AB∥B′C，
理由是：∵θ=30°，∠ACB=90°，
∴∠A′CB′=90°，
∴∠BCB′=90°-60°=30°，
∵∠B=30°，
∴∠B=∠BCB′，
∴AB∥B′C；

（2）△A′CD的形状是等边三角形，
理由是：∵∠ACB=90°，∠B=30°，
∴∠A=180°-90°-30°=60°，
∴∠A′=∠A=60°，
∴∠A′=∠A′CD=60°，
∴A′D=CD，
∴△A′CD是等边三角形；
（3）连结CP，如图1，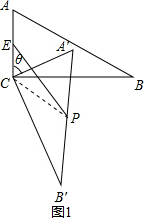
∵∠ACB=90°，∠ABC=30°，
∴AB=2AC=2a，
∵E为AC的中点，
∴CE=$\frac{1}{2}$a，
∵△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），
∴A′B′=AB=2a，
∵点P为A′B′的中点，
∴CP=$\frac{1}{2}$A′B′=a，
∵PE＜CE+PC，
∴只有当点P在EC的延长线上时，PE=CE+PC，此时PE最大，如图2，
即PE的最大值为$\frac{1}{2}$a+a=$\frac{3}{2}$a，
此时θ=∠P′CB+∠BCP=30°+90°=120°，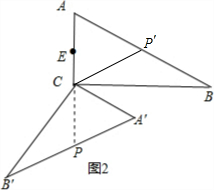
故答案为：120°，$\frac{3}{2}$a．

点评 本题考查了等边三角形的判定，平行线的判定，旋转的性质的应用，注意：旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了直角三角形斜边上的中线性质．