题目内容
二次函数y=(k-1)x2+(2k-1)x+k-2与x轴有两个交点,则k的取值范围是 .
考点:抛物线与x轴的交点
专题:探究型
分析:根据二次函数y=(k-1)x2+(2k-1)x+k-2与x轴有两个交点可知△≥0,由△≥0可得出关于k的不等式,求出k的取值范围即可.
解答:解:∵二次函数y=(k-1)x2+(2k-1)x+k-2与x轴有两个交点,
∴△≥0,k-1≠0,即
,解得k≥
且k≠1.
故答案为:k≥
且k≠1.
∴△≥0,k-1≠0,即
|
| 7 |
| 8 |
故答案为:k≥
| 7 |
| 8 |
点评:本题考查的是抛物线与x轴的交点及二次函数的定义,此题中k-1≠0是易忽略的地方.

练习册系列答案
相关题目
 如图,D为△ABC的BC边的中点,E为AC边上的一点,AC=3CE,BE和AD交于G点,则AG:GD=( )
如图,D为△ABC的BC边的中点,E为AC边上的一点,AC=3CE,BE和AD交于G点,则AG:GD=( )| A、2 | B、3 | C、3或4 | D、4 |
 已知AD、BE、CF为△ABC的三条高(D、E、F为垂足),∠ABC=45°,∠C=60°,则
已知AD、BE、CF为△ABC的三条高(D、E、F为垂足),∠ABC=45°,∠C=60°,则| DE |
| DF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,AD⊥AB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD=CE.
如图,AD⊥AB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD=CE.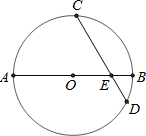 如图,AB是⊙O的直径,弦CD与AB相交于点E,AE=13,BE=3,cos∠AEC=
如图,AB是⊙O的直径,弦CD与AB相交于点E,AE=13,BE=3,cos∠AEC=