题目内容
9.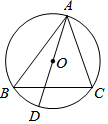 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 连接CD,则可得∠ACD=90°,且∠B=∠D,在Rt△ADC中可求得CD,则可求得cosD,即可求得答案.
解答  解:
解:
如图,连接CD,
∵AD⊙O的直径,
∴∠ACD=90°,且∠B=∠D,
在Rt△ACD中,AD=5×2=10,AC=8,
∴CD=6,
∴cosD=$\frac{CD}{AD}$=$\frac{6}{10}$=$\frac{3}{5}$,
∴cosB=cosD=$\frac{3}{5}$,
故选B.
点评 本题主要考查圆周角定理及三角函数的定义,构造直角三角形是解题的关键.

练习册系列答案
相关题目
19.用配方法解方程x2-4x-5=0时,原方程应变形为( )
| A. | (x-2)2=9 | B. | (x-1)2=6 | C. | (x+1)2=6 | D. | (x+2)2=6 |
20. 如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD.
 如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
如图,下列选项中能使平行四边形ABCD是菱形的条件有( )①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD.
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
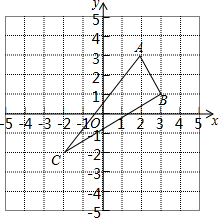 △ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(-2,-2)三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(-2,-2)三点在格点上. 在数学课上,老师请同学思考如下问题:
在数学课上,老师请同学思考如下问题: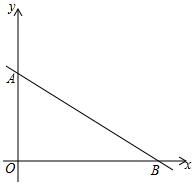 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.