题目内容
14.已知一次函数y=-2x+1的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数y=$\frac{k}{x}$(k≠0)图象在第二象限内的交点.(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,直接写出点C的坐标.
分析 (1)由点B的横坐标利用一次函数图象上点的坐标特征即可求出点B的坐标,根据点B的坐标利用反比例函数图象上点的坐标特征即可求出k值;
(2)令x=0利用一次函数图象上点的坐标特征可求出点A的坐标,设点C的坐标为(m,0),根据两点间的距离公式结合AC=AB即可得出关于m无理方程,解之即可得出m的值,进而得出点C的坐标.
解答 解:(1)∵点B(-1,n)在直线y=-2x+1上,
∴n=2+1=3.
∴点B的坐标为(-1,3).
∵点B(-1,3)在反比例函数$y=\frac{k}{x}$的图象上,
∴k=-3.
(2)当x=0时,y=-2x+1=1,
∴点A的坐标为(0,1).
设点C的坐标为(m,0),
∵AC=AB,
∴$\sqrt{{m}^{2}+1}$=$\sqrt{(-1-0)^{2}+(3-1)^{2}}$=$\sqrt{5}$,
解得:m=±2.
∴点C的坐标为(2,0)或(-2,0).
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征以及反比例函数图象上点的坐标特征,根据一次函数图象上点的坐标特征找出点A、B的坐标是解题的关键.

练习册系列答案
相关题目
4.关于一次函数y=-2x+b(b为常数),下列说法正确的是( )
| A. | y随x的增大而增大 | |
| B. | 当b=4时,直线与坐标轴围成的面积是4 | |
| C. | 图象一定过第一、三象限 | |
| D. | 与直线y=3-2x相交于第四象限内一点 |
9.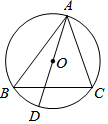 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
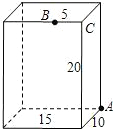 如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,徐亚爬行的最短距离是25cm.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,徐亚爬行的最短距离是25cm.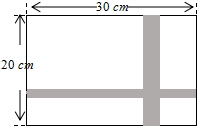 如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm? 如图所示的钟表,表盘上均匀分布着60条刻度线,若时针和分针分别指向两条相邻的刻度线,则钟表在0点-12点中所表示的时间可能是2点12分或9点48分.
如图所示的钟表,表盘上均匀分布着60条刻度线,若时针和分针分别指向两条相邻的刻度线,则钟表在0点-12点中所表示的时间可能是2点12分或9点48分.